
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】(1)AB=5;C(8,0).(2)y=![]() x﹣6;(3)P点的坐标为(0,12)或(0,﹣4).
x﹣6;(3)P点的坐标为(0,12)或(0,﹣4).
【解析】
(1)先求得点A和点B的坐标,则可得到OA、OB的长,然后依据勾股定理可求得AB的长,然后依据翻折的性质可得到AC的长,于是可求得OC的长,从而可得到点C的坐标;
(2)设OD=x,则CD=DB=x+4.,Rt△OCD中,依据勾股定理可求得x的值,从而可得到点D(0,﹣6),然后利用待定系数法求解即可;
(3)先求得S△PAB的值,然后依据三角形的面积公式可求得BP的长,从而可得到点P的坐标.
解:(1)令x=0得:y=4,
∴B(0,4).
∴OB=4
令y=0得:0=﹣![]() x+4,解得:x=3,
x+4,解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,AB=![]() =5.
=5.
∴OC=OA+AC=3+5=8,
∴C(8,0).
(2)设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,解得:x=6,
∴D(0,﹣6).
设CD的解析式为y=kx﹣6,将C(8,0)代入得:8k﹣6=0,解得:k=![]() ,
,
∴直线CD的解析式为y=![]() x﹣6.
x﹣6.
(3)∵S△PAB=![]() ,
,
∴S△PAB=![]() ×
×![]() ×6×8=12.
×6×8=12.
∵点Py轴上,S△PAB=12,
∴![]() BPOA=12,即
BPOA=12,即![]() ×3BP=12,解得:BP=8,
×3BP=12,解得:BP=8,
∴P点的坐标为(0,12)或(0,﹣4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在![]() 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校![]() 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题: 
(1)本次抽样调查的样本容量是 , 表示“D级(不喜欢)”的扇形的圆心角为°;
(2)若该校九年级有200名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;
(3)若从本次调查中的A级(非常喜欢)的5名学生中,选出2名去参加广州市中学生诗词大会比赛,已知A级学生中男生有3名,请用“列表”或“画树状图”的方法求出所选出的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在Rt△ABC中,斜边AB=10,sinA= ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.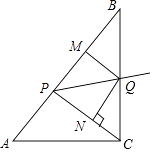
(1)当AP=CP时,求QP;
(2)若四边形PMQN为菱形,求CQ;
(3)探究:AP为何值时,四边形PMQN与△BPQ的面积相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国国家邮政局公布的数据显示,2016年中国快递业务量突破313.5亿件,同比增长51.7%,快递业务量位居世界第一,业内人士表示,快递业务连续6年保持50%以上的高速增长,已成为中国经济的一匹“黑马”,未来中国快递业务仍将保持快速增长势头,以下是根据相关数据绘制的统计图,请你预估2017年全国快递的业务量大约为(精确的0.1)亿元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1. 
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 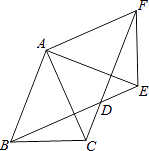
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y1=k1x(k1>0)与反比例函数y2= ![]() (k2>0)部分图象如图所示,则不等式k1x>
(k2>0)部分图象如图所示,则不等式k1x> ![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com