
【题目】如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1. 
(1)求∠BAM的度数;
(2)求正方形ABCD的边长.
【答案】
(1)解:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
∵AM=AN,
在Rt△ABM和Rt△ADN中,
![]() ,
,
∴△ABM≌△ADN(HL),
∴∠BAM=∠DAN,
∵∠MAN=30°,∠BAD=90°,
∴∠BAM=30°.
(2)解:作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,
∵ ![]() ANMH=1,
ANMH=1,
∴ ![]() 2xx=1,
2xx=1,
解得x=1或﹣1(舍弃),
∴AB= ![]() BM=
BM= ![]() ,
,
∴正方形ABCD的边长为 ![]() .
.
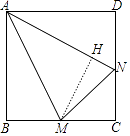
【解析】(1)只要证明△ABM≌△ADN(HL),推出∠BAM=∠DAN,由∠MAN=30°,∠BAD=90°,即可推出∠BAM=30°;(2)作MH⊥AN于H.设BM=x,则AM=AN=2x,MH=x,根据 ![]() ANMH=1,列出方程即可;
ANMH=1,列出方程即可;
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
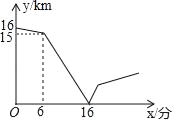
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(km)与甲出发的时间x(分)之间的关系如图所示.
(1)求甲、乙相遇时,乙所行驶的路程;
(2)当乙到达终点A时,甲还需多少分钟到达终点B?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( ) 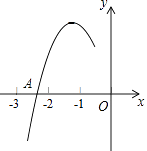
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AD是BC边上的中线,点E是AD的中点;过点A作AF∥BC,交BE的延长线于F,连接CF. 
(1)求证:四边形ADCF是平行四边形;
(2)填空: ①当AB=AC时,四边形ADCF是形;
②当∠BAC=90°时,四边形ADCF是形.
查看答案和解析>>
科目:初中数学 来源: 题型:
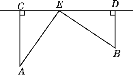
【题目】(方程思想)如图,在铁路CD同侧有两个村庄A,B,它们到铁路的距离分别是15 km和10 km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25 km.已知铁路旁有一个农副产品收购站E,且AE=BE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=﹣x2+(2m+2)x﹣(m2+4m﹣3)中,m为不小于0的整数,它的图象与x轴的交点A在原点左边,交点B在原点右边.
(1)求这个二次函数的解析式;
(2)设点C为此二次函数图象上的一点,且满足△ABC的面积等于10,请求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 若a2=b2,则a=b B. 若∠1+∠2=90,则∠1与∠2互余
C. 若∠α与∠β是同位角,则∠α=∠β D. 若a⊥b,b⊥c,则a⊥c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com