
【题目】如图,已知:在Rt△ABC中,斜边AB=10,sinA= ![]() ,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.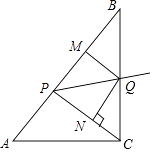
(1)当AP=CP时,求QP;
(2)若四边形PMQN为菱形,求CQ;
(3)探究:AP为何值时,四边形PMQN与△BPQ的面积相等?
【答案】
(1)
解:∵AB=10,sinA= ![]() ,
,
∴BC=8,
则AC= ![]() =6,
=6,
∵PA=PC.
∴∠PAC=∠PCA,
∵PQ平分∠CPB,
∴∠BPC=2∠BPQ=2∠A,
∴∠BPQ=∠A,
∴PQ∥AC,
∴PQ⊥BC,又PQ平分∠CPB,
∴∠PCQ=∠PBQ,
∴PB=PC,
∴P是AB的中点,
∴PQ= ![]() AC=3;
AC=3;
(2)
解:∵四边形PMQN为菱形,
∴MQ∥PC,
∴∠APC=90°,
∴ ![]() ×AB×CP=
×AB×CP= ![]() ×AC×BC,
×AC×BC,
则PC=4.8,
由勾股定理得,PB=6.4,
∵MQ∥PC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CQ= ![]() ;
;
(3)
解:∵PQ平分∠CPB,QM⊥AB,QN⊥CP,
∴QM=QN,PM=PN,
∴S△PMQ=S△PNQ,
∵四边形PMQN与△BPQ的面积相等,
∴PB=2PM,
∴QM是线段PB的垂直平分线,
∴∠B=∠BPQ,
∴∠B=∠CPQ,
∴△CPQ∽△CBP,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CP=4× ![]() =4×
=4× ![]() =5,
=5,
∴CQ= ![]() ,
,
∴BQ=8﹣ ![]() =
= ![]() ,
,
∴BM= ![]() ×
× ![]() =
= ![]() ,
,
∴AP=AB﹣PB=AB﹣2BM= ![]() .
.
【解析】(1)根据正弦的概念求出BC,根据勾股定理求出AC,根据三角形中位线定理计算即可;(2)根据菱形的性质得到MQ∥PC,根据相似三角形的性质列出比例式,计算即可;(3)根据角平分线的性质得到QM=QN,PM=PN,根据题意得到PB=2PM,得到QM是线段PB的垂直平分线,根据垂直平分线的性质、相似三角形的判定定理解答.
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是![]() ,则“宝藏”点的坐标是( )
,则“宝藏”点的坐标是( )
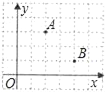
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( ) 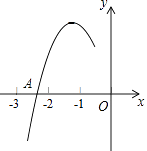
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AD是BC边上的中线,点E是AD的中点;过点A作AF∥BC,交BE的延长线于F,连接CF. 
(1)求证:四边形ADCF是平行四边形;
(2)填空: ①当AB=AC时,四边形ADCF是形;
②当∠BAC=90°时,四边形ADCF是形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④对任意实数x均有ax2+bx≥a+b
正确的结论序号为: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com