
【题目】数学活动课上,老师提出了一个问题:
我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?
(1)独立思考,请你完成老师提出的问题:
如图所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.

解:
⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图所示),那么∠A与∠F之间有何数量关系?请写出解答过程.

【答案】(1)∠DBC+∠BCE-∠A=180(2)![]() ∠A+∠F=90
∠A+∠F=90
【解析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,三角形内角和定理计算即可.
(2)根据角平分线可知∠FBC+∠FCB=![]() (∠DBC+∠BCE,)再根据三角形内角和定理,结合(1)即可解答.
(∠DBC+∠BCE,)再根据三角形内角和定理,结合(1)即可解答.
⑴∠DBC+∠BCE-∠A=180.
∠DBC+∠BCE
=∠ABC+∠A+∠ACB+∠A
=180°+∠A
即∠DBC+∠BCE-∠A=180.
(2)![]() ∠A+∠F=90°
∠A+∠F=90°
∵BF和CF分别平分∠CBD和∠BCE,
∴∠CBF=![]() ∠CBD,∠BCF=
∠CBD,∠BCF=![]() ∠BCE.
∠BCE.
∴∠CBF+∠BCF=![]() (∠CBD+∠BCE).
(∠CBD+∠BCE).
∵∠CBF+∠BCF=180-∠F,∠DBC+∠BCE=180+∠A.
∴180-∠F =![]() (∠CBD+∠BCE)=
(∠CBD+∠BCE)=![]() (180+∠A)
(180+∠A)
∴![]() ∠A+∠F=90.
∠A+∠F=90.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
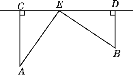
【题目】(方程思想)如图,在铁路CD同侧有两个村庄A,B,它们到铁路的距离分别是15 km和10 km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25 km.已知铁路旁有一个农副产品收购站E,且AE=BE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 若a2=b2,则a=b B. 若∠1+∠2=90,则∠1与∠2互余
C. 若∠α与∠β是同位角,则∠α=∠β D. 若a⊥b,b⊥c,则a⊥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线, 
(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上. 
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?答: .
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下管道,若由甲队单独铺设,恰好在规定时间内完成;若由乙队单独铺设,需要超过规定时间15天才能完成,如果先由甲、乙两队合做10天,再由乙队单独铺设正好按时完成.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为5000元,乙队每天的施工费用为3000元,为了缩短工期以减少对居民交通的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,那么该工程施工费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com