
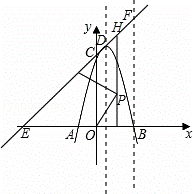
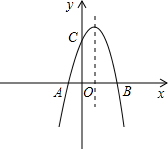
如图,已知抛物线与x轴交于点A(﹣2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?

解:(1)设抛物线解析式为y=a(x+2)(x﹣4).
把C(0,8)代入,得a=﹣1.
∴y=﹣x2+2x+8=﹣(x﹣1)2+9,
顶点D(1,9);(2分)
(2)假设满足条件的点P存在.依题意设P(2,t).
由C(0,8),D(1,9)求得直线CD的解析式为y=x+8,
它与x轴的夹角为45°.
设OB的中垂线交CD于H,则H(2,10).
则PH=|10﹣t|,点P到CD的距离为![]() .
.
又![]() .(4分)
.(4分)
∴![]() .
.
平方并整理得:t2+20t﹣92=0,解之得t=﹣10±8![]() .
.
∴存在满足条件的点P,P的坐标为(2,﹣10±8![]() ).(6分)
).(6分)
(3)由上求得E(﹣8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=﹣x2+2x+8+m(m>0).
当x=﹣8时,y=﹣72+m.
当x=4时,y=m.
∴﹣72+m≤0或m≤12.
∴0<m≤72.(8分)
②若抛物线向下平移,可设解析式为y=﹣x2+2x+8﹣m(m>0).
由![]() ,
,
有﹣x2+x﹣m=0.
∴△=1+4m≥0,
∴m≥﹣![]() .
.
∴向上最多可平移7![]() 2个单位长,向下最多可平移
2个单位长,向下最多可平移![]() 个单位长.(10分)
个单位长.(10分)


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
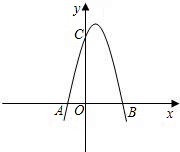 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:
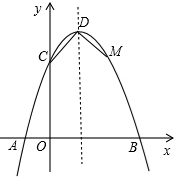 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1查看答案和解析>>
科目:初中数学 来源: 题型:
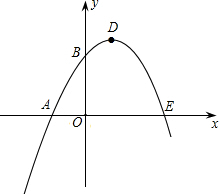 函数的最大值是4.
函数的最大值是4.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com