
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.

(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
【答案】(1)AB= 6;(2)没有最大值,理由见解析.
【解析】(1)由等边三角形的性质容易得出结果;
(2)设CD=PC=PD=x,则EF=EP=PF=6﹣x,求出等边△CDP和△EFP的面积之和S=![]() x2﹣3
x2﹣3![]() x+9
x+9![]() >0,得出S有最小值,没有最大值.
>0,得出S有最小值,没有最大值.
(1)∵△CDP和△EFP是等边三角形,∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF.
∵DF=PD+PF=2,∴AB=AP+BP=3DF=3×2=6;
(2)没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF=![]() (18﹣3x)=6﹣x,作CM⊥PD于M,EN⊥PF于N,则DM=
(18﹣3x)=6﹣x,作CM⊥PD于M,EN⊥PF于N,则DM=![]() PD=
PD=![]() x,PN=
x,PN=![]() PF=
PF=![]() (6﹣x),∴CM=
(6﹣x),∴CM=![]() DM=
DM=![]() x,EN=
x,EN=![]() (6﹣x),
(6﹣x),
∴△CDP的面积=![]() PDCM=
PDCM=![]() x2,△EFP的面积=
x2,△EFP的面积=![]() (6﹣x)2,
(6﹣x)2,
∴等边△CDP和△EFP的面积之和S=![]() x2+
x2+![]() (6﹣x)2=
(6﹣x)2=![]() x2﹣3
x2﹣3![]() x+9
x+9![]() .
.
∵![]() >0,∴S有最小值,没有最大值.
>0,∴S有最小值,没有最大值.



科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长60cm,一根长100cm,将它们的一个端点重合,放在同一条直线上,此时两根木条中点间的距离( )
A.20cmB.80cm
C.160cmD.20cm 或80cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当A落在四边形BCDE内时,则∠A与∠1+∠2之间有始终不变的关系是( )

A.∠A=∠1+∠2B.2∠A=∠1+∠2
C.3A=∠1+∠2D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)找规律:1,2,4,8……,则第n个数为________.
(2)求和![]() ,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设:
,观察发现,从第2个加数起每一个加数都是前一个加数的2倍.于是可假设:![]() ①
①
两边乘以2得:![]() ②
②
②-①得:![]() ,所以:
,所以:![]()
类比做一做,求![]() 的值.
的值.
(3)仿照(2)的做法求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级![]() 名学生进行测试,并把测试成绩(单位:
名学生进行测试,并把测试成绩(单位:![]() ) 绘制成不完整的频数分布表和频数分布直方图.
) 绘制成不完整的频数分布表和频数分布直方图.
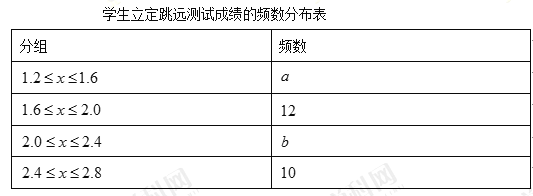

请根据图表中所提供的信息,完成下列问题
(1)表中![]() = ,
= ,![]() = ;
= ;
(2)请把频数分布直方图补充完整;
(3)跳远成绩大于等于![]() 为优秀,若该校九年级共有
为优秀,若该校九年级共有![]() 名学生,估计该年级学生立定跳远成绩优秀的学生有多少人?
名学生,估计该年级学生立定跳远成绩优秀的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
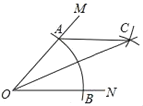
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(原题)已知直线AB∥CD,点P为平行线AB,CD之间的一点.如图1,若∠ABP=50°,∠CDP=60°,BE平分∠ABP,DE平分∠CDP,求∠BED的度数.
(探究)如图2,当点P在直线AB的上方时,若∠ABP=α,∠CDP=β,∠ABP和∠CDP的平分线交于点E1,∠ABE1与∠CDE1的角平分线交于点E2,∠ABE2与∠CDE2的角平分线交于点E3,…以此类推,求∠En的度数.
(变式)如图3,∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E,试猜想∠P与∠E的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com