
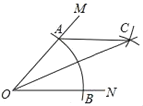
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
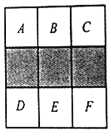
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
四、解答题(二):本大题共5小题,共50分.解答应写出文字说明、证明过程或演算步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.

(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌运动鞋经销商购进A、B两种新式运动鞋,按标价售出后可获利48000元.已知购进A种运动鞋的数量是B种运动鞋数量的2倍,这两种运动鞋的进价、标价如下表所示.
款式 价格 | A | B |
进价(元/双) | 100 | 120 |
标价(元/双) | 250 | 300 |
(1)这两种运动鞋各购进多少双?
(2)如果A种运动鞋按标价9折出售,B种运动鞋按标价8折出售,那么这批运动鞋全部售出后,经销商所获利润比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需18元;3只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共40只,并且A型节能灯的数量不多于B型节能
灯数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0其中正确的是( ).
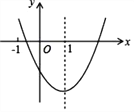
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
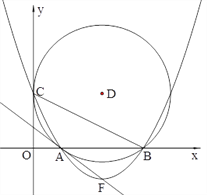
【题目】如图24,在平面直角坐标系中,圆D与![]() 轴相切于点C(0,4),与
轴相切于点C(0,4),与![]() 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6
(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在![]() 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使![]() 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出![]() 点坐标.
点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com