
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
【答案】(1)共有4种方案,具体方案见解析;(2)购买A型设备2台、B型设备8台时费用最少.
【解析】(1)设该景区购买A种设备为x台、则B种设备购买(10-x)台,其中 0 ≤x ≤10,根据购买的设备日处理能力不低于140吨,列不等式,求出解集后再根据x的范围以及x为整数即可确定出具体方案;
(2)针对(1)中的方案逐一进行计算即可做出判断.
(1)设该景区购买设计 A型设备为x台、则 B型设备购买(10-x)台,其中 0 ≤x ≤10,
由题意得:12x+15(10-x)≥140,
解得x≤![]() ,
,
∵0 ≤x ≤10,且x是整数,
∴x=3,2,1,0,
∴B型相应的台数分别为7,8,9,10,
∴共有4种方案:
方案一:A型设备 3 台、B型设备 7 台;
方案二:A型设备 2 台、B型设备 8 台;
方案三:A型设备 1 台、B型设备 9 台;
方案四:A型设备 0 台、B型设备 10 台.
(2)方案二费用最少,理由如下:
方案一购买费用: 3 ×3+4.4 ×7=39.8 (万元)<40 (万元),∴费用为 39.8(万元);
方案二购买费用: 2 ×3+4.4 ×8=41.2 (万元)>40 (万元),
∴ 费用为 41.2 ×90%=37.08(万元);
方案三购买费用:3 ×1+4.4 ×9=42.6 (万元)>40 (万元),
∴ 费用为 42.6 ×90%=38.34(万元);
方案四购买费用:4.4 ×10=44 (万元)>40 (万元), ∴ 费用为 44 ×90%=39.6(万元).
∴方案二费用最少,即A型设备2台、B型设备8台时费用最少.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
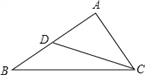
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.
【答案】5![]() .
.
【解析】试题分析:
由点D是AB的中点,AB=10,易得AD=5;再由∠ACD=∠B,∠A=∠A,可证得:
△ACD∽△ABC,从而可得: ![]() ,由此得到:AC2=AD
,由此得到:AC2=AD![]() AB=50即可解得AC的值.
AB=50即可解得AC的值.
试题解析:
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC.
∴![]() ,
,
∴AC2=AD![]() AB.
AB.
∵D是AB的中点,AB=10,
∴AD=![]() AB=5,
AB=5,
∴AC2=50.
解得AC=![]() .
.
【题型】解答题
【结束】
22
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
(1)求抛物线所对应的函数解析式;
(2)求ΔABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某汽车行驶的路程![]()
![]() 与时间
与时间![]() (分钟)的函数关系图.
(分钟)的函数关系图.

观察图中所提供的信息,解答下列问题:
(1)汽车在前![]() 分钟内的平均速度是 .
分钟内的平均速度是 .
(2)汽车在中途停了多长时间?
(3)当![]() 时,求
时,求![]() 与
与![]() 的函数关系式
的函数关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课余生活,我校准备开设兴趣课堂.为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况,在全校进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题:

(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果我校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△AOB中,∠AOB=90°,以顶点O为原点,分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系(如图),点A(a,0),B(0,b)满足![]() +|a-2|=0
+|a-2|=0

(1)点A的坐标为 ;点B的坐标为 .
(2)如图①,已知坐标轴上有两动点D、E同时出发,点D从A点出发沿x轴负方向以每秒1个单位长度的速度匀速移动,点E从O点出发以每秒2个单位长度的速度沿y轴正方向移动,点E到达B点时运动结束,AB的中点C的坐标是(1,2),设运动时间为t(t>0)秒,问:是否存在这样的t,使S△OCD=S△OCE?若存在,请求出t的值:若不存在,请说明理由.
(3)如图②,点F是线段AB上一点,满足∠FOA=∠FAO,点G是第二象限中一点,连OG使得∠BOG=∠BOF,点P是线段OB上一动点,连AP交OF于点Q,当点P在线段OB上运动的过程中,![]() 的值是否会发生变化?若不变,请求出k的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出k的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com