
【题目】如图(1),等边△ABC 中,D 是 AB 边上的动点,以 CD 为一边,向上作等边△EDC,连接AE.
(1)△DBC 和△EAC 会全等吗?请说说你的理由;
(2)试说明 AE∥BC 的理由;
(3)如图(2),将(1)动点 D 运动到边 BA 的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
【答案】
(1)解:△DBC≌△EAC ,理由如下:
∵△ABC、△EDC均为等边三角形,
∴∠ACB=∠DCE=60°,
∴∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD,
∴∠BCD=∠ACE
在△DBC 和△EAC 中,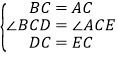
∴△DBC≌△EAC(SAS).
(2)解:由(1)知△DBC≌△EAC,
∴∠EAC=∠B=60° ,
又∵∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
(3)解:AE∥BC 仍然成立;理由如下:
∵△ABC、△EDC 为等边三角形,
∴BC=AC,DC=CE,∠BCA=∠DCE=60°,
又∵∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD,
∴∠BCD=∠ACE,
在△DBC 和△EAC 中,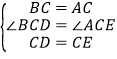
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60° ,
又∵∠ACB=60°,
∴∠EAC=∠ACB,
∴AE∥BC.
【解析】(1)△DBC≌△EAC ,理由如下:由等边三角形的性质得出∠ACB=∠DCE=60°,再根据等量代换求出∠BCD=∠ACE;最后根据SAS得△DBC≌△EAC.
(2)由(1)知△DBC≌△EAC,根据全等三角形的对应角相等得出∠EAC=∠B=60° ,又∠ACB=60°,等量代换得出∠EAC=∠ACB,根据内错角相等,两直线平行,从而得证.
(3)AE∥BC 仍然成立;理由如下:由等边三角形的性质得出BC=AC,DC=CE,∠BCA=∠DCE=60°,再根据等量代换求出∠BCD=∠ACE;最后根据SAS得△DBC≌△EAC;再根据全等三角形的对应角相等得出∠EAC=∠B=60° ,又∠ACB=60°,等量代换得出∠EAC=∠ACB,根据内错角相等,两直线平行,从而得证.
【考点精析】掌握平行线的判定和等边三角形的性质是解答本题的根本,需要知道同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;等边三角形的三个角都相等并且每个角都是60°.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】若三个非零实数![]() 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数
满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数![]() 构成“和谐三数组”.
构成“和谐三数组”.
(1)实数1,2,3可以构成“和谐三数组”吗?请说明理由.
(2)若![]() 三点均在函数y=
三点均在函数y=![]() (
(![]() 为常数,
为常数,![]() )的图象上,且这三点的纵坐标
)的图象上,且这三点的纵坐标![]() 构成“和谐三数组”,求实数
构成“和谐三数组”,求实数![]() 的值;
的值;
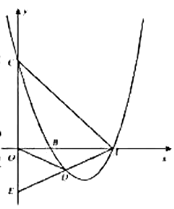
(3)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点.
两点.
①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;
②若a>2b>3c,x2=1,求点P(,)与原点O的距离OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
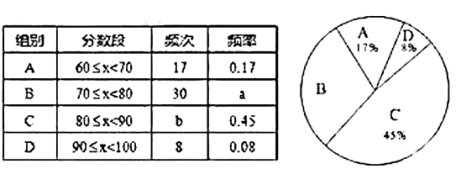
请根据所给信息,解答以下问题:
(1)表中![]() ;
;![]() ;
;
(2)请计算扇形统计图中![]() 组对应的圆心角的度数;
组对应的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图,按规定∠A= 90°,∠B、∠C 分别是 32°和 21°.某检验工人量得∠BDC= 148°,就断定这个零件不合格,试用三角形的有关知识说明零件不合格的理由.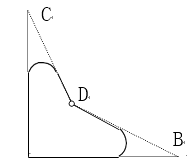
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以下列三个数为边长的三角形中,不能组成直角三角形的是( )
A. 4、7、9 B. 5、12、13 C. 6、8、10 D. 7、24、25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC,DE⊥AB,D是AB的中点,DE交AC于E点,连结BE,BC=10cm,
△BEC的周长是24cm,那么AB的长是 . 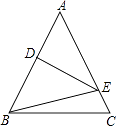
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
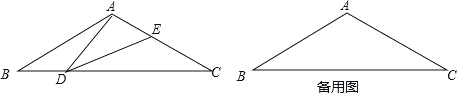
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com