
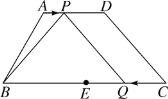
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC��60�㣬AB��8��BC��16��AD��6.E��BC���е㣬��P��ÿ��1����λ���ȵ��ٶȴӵ�A��������AD���D�˶�����Qͬʱ��ÿ��2����λ���ȵ��ٶȴӵ�C��������CB���B�˶�����Pֹͣ�˶�ʱ����QҲ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮
(1)���BPQ�����ΪS����S��t֮��ĺ�����ϵʽ��
(2)��t��________ʱ����BPQ��������ı���PQCD�������ȣ�
(3)��tΪ��ֵʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�
���𰸡�(1) S=��4![]() t��32
t��32![]() (0��t��6)�� (2)
(0��t��6)�� (2)![]() ��(3) 2��
��(3) 2��![]() ��
��
��������(1)����A��AF��BC�ڵ�F�����AFB��90�����ɺ�30��ǵ�ֱ�������ε����ʼ����ɶ����õ�AF�ij������������ε������ʽ���ɵõ����ۣ�
(2)��S��S�ı���PQCD ��S�ı���ABCD��S��BPQ��S��ABP����ʾ�������ֵ���������빫ʽ�ⷽ�̼��ɣ�
(3)����������������ı���PEQD���ı���PQEDΪƽ���ı��Σ��õ�PD��EQ��
��PD��6��t��EQ��8��2t��2t��8������ⷽ�̼��ɣ�
(1)����A��AF��BC�ڵ�F�����AFB��90����
�ߡ�ABC��60�������BAF��30����
��AB��8����BF��![]() AB��4����AF��
AB��4����AF��![]() ��
��![]() ��
��
�߾���t���BQ��16��2t����S��![]() ��BQ��AF��
��BQ��AF��![]() ��(16��2t)��
��(16��2t)��![]() ����
����![]() t��
t��![]() (0��t��6)��
(0��t��6)��
(2)��ͼ��֪S�ı���PQCD��S�ı���ABCD��S��BPQ��S��ABP��
��AP��t����S��ABP��![]() AP��AF��
AP��AF��![]() ��
��
�֡�S�ı���ABCD��![]() AF(AD��BC)��
AF(AD��BC)��![]() ��
��![]() ��(6��16)��
��(6��16)��![]() ����S�ı���PQCD��
����S�ı���PQCD��![]() ��(��
��(��![]() t��
t��![]() )��
)��![]() ��
��![]() ��
��
��S��S�ı���PQCD����![]() ����
����![]() t��
t��![]() ����ã�t��
����ã�t��![]() ��
��
(3)�������֪�ı���PEQD���ı���PQEDΪƽ���ı��Σ���PD��EQ��
��PD��6��t��EQ��8��2t��2t��8����6��t��8��2t��6��t��2t��8����ã�t��2��t��![]() ��
��
�ʵ�t��2��![]() ʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�
ʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�β���У�ijͬѧվ�ڵ�A���۲�ͣ����B��C������С������ô�B�ڵ�A��ƫ��75������150�״�����C�ڵ�A��ƫ��15������120�״�����B�봬C֮��ľ���Ϊ______�ף���ȷ��0.1![]() ����
����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ�������ıϴ����˹ѧ�ɰ�1��3��6��10������������Ϊ������������������1��4��9��16������������Ϊ����������������ͼ�п��Է��֣��κ�һ������1�������������������Կ�����������������������֮�ͣ����е�ʽ�У�������һ���ɵ��ǣ�������

A. 13=3+10 B. 25=9+16 C. 36=15+21 D. 49=18+31
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
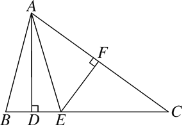
����Ŀ����ͼ����ABC�У�AD��BC�ڵ�D��EF��ֱƽ��AC����AC�ڵ�F����BC�ڵ�E����BD��DE������AE.
(1)����BAE��30�㣬���C�Ķ�����
(2)����ABC���ܳ�Ϊ13cm��AC��6cm����DC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͺ��͵��϶�����������A�ص�B��ȼ����ʻ��ȼ�ͷ���76Ԫ����A�ص�B���õ���ʻ�������26Ԫ����֪ÿ��ʻ1ǧ�ף���ȼ�ͷ��ñȴ��õ���ö�0.5Ԫ��
��1����ÿ��ʻ1ǧ�״��õ�ķ��ã�
��2����Ҫʹ��A�ص�B���͵�����ʻ������͡�����úϼƲ�����39Ԫ���������õ���ʻ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ����ͼ���ֱ�������������ƴ�ɣ�����a��b��
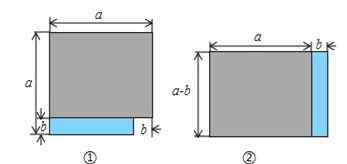
��1���ú�a��b�Ĵ���ʽ��ʾ���ǵ��������S��= ��S��= + ��
��2��S����S��֮���������Ĵ�С��ϵ������������еĵ�����
��3�����������������ֵĽ��ۼ���ʽ�ӣ�20182��20172��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ�˽Ȿ�еĿ���������������л����������ȡ��������Ŀ������������Ϊ�걾����ͳ�ƣ����Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������ϢΪ������
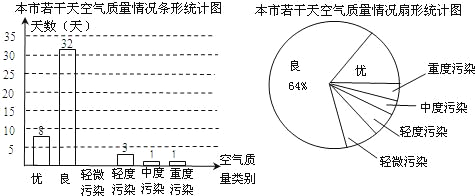
�������ͼ���ṩ����Ϣ������������⣺
��1�����ε����й���ȡ�˶�����Ŀ������������Ϊ�걾��
��2��������Ⱦ��������ȫ����ͳ��ͼ��
��3��������Ƹ�����һ�꣨365�죩���������ﵽ������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A������Ϊ����2��0�����ȱ�������AOC����ƽ������Գƻ���ת�Գƶ����Եõ���OBD��
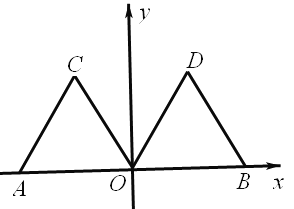
��1����AOC��x������ƽ�Ƶõ���OBD����ƽ�Ƶľ����� ����λ���ȣ���AOC����OBD����ֱ�߶Գƣ���Գ����� ����AOC��ԭ��O˳ʱ����ת�õ���OBD������ת�ǿ����� �ȣ�
��2������AD����OC�ڵ�E������AEO�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������֮��ľ���������ľ���ֵ�����ǿ����ñ�ʾ��������Ĵ�д��ĸһ���ǣ����磬��ʾ��A����Ϊ2����B��ʾ����Ϊ��3����A���B֮��ľ������AB����AB=2������3��=5��
��1�������ϱ�ʾ��3��5������֮��ľ�������
��2����ͼ���������ϵ�A��ʾ��a����C��ʾ��c����|a+20|+��c��30��2=0�����A���C֮��ľ���AC��
��3���ڣ�2���������£����������Ƿ���ڵ�B��ʹAB=5�������ڣ������B��ʾ����b���������ڣ���˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com