
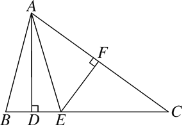
【题目】如图,△ABC中,AD⊥BC于点D,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)若∠BAE=30°,求∠C的度数;
(2)若△ABC的周长为13cm,AC=6cm,求DC的长.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) 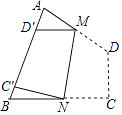
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一组数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,将这组数排成如图的形式,
第一行 -1
第二行 2 -3 4
第三行 -5 6 -7 8 -9
第四行 10 -11 12 -13 14 -15 16
按照如图规律排下去,(1)第10行中从左边数第4个数是__________;(2)前7行的数字总和是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=![]() =5050.
=5050.
(1)补全例题![]() 解题过程;
解题过程;
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
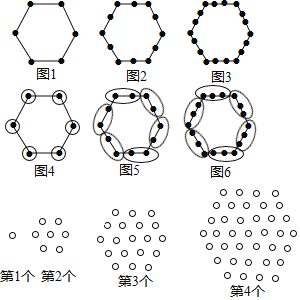
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
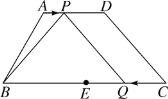
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=60°,AB=8,BC=16,AD=6.E是BC的中点,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t=________时,△BPQ的面积与四边形PQCD的面积相等;
(3)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 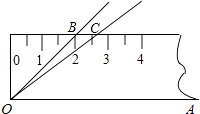
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图) 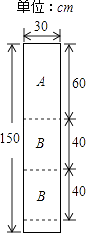
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 2 | m | n |
(1)上表中,m= , n=;
(2)若裁完剩余的部分可以拼接成A型或B型板材使用,则至少需要几张标准板材?
(3)若裁完剩余的部分不能拼接成A型或B型板材使用,已知用170张标准板材,可以完成装修任务.请通过计算写出两种剪裁方案(要求:①其中一种方案三种剪裁方法都使用,另一种方案只用到两种剪裁方法;②每种方案需写出使用各种裁剪方法裁剪标准板的张数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com