
【题目】如图1,![]() 点是第二象限内一点,
点是第二象限内一点,![]() 轴于
轴于![]() ,且
,且![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() 是x轴负半
是x轴负半![]() 轴上一点,且
轴上一点,且![]() .
.

(1)![]() ( ),
( ),![]() ( )
( )
(2)如图2,设![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,
时,![]() 的角平分线与
的角平分线与![]() 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点![]() ,求
,求![]() 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为![]() )
)
(3)如图3,当![]() 点在线段
点在线段![]() 上运动时,作
上运动时,作![]() 交
交![]() 于
于![]() 的平分线交于
的平分线交于![]() ,当
,当![]() 点在运动的过程中,
点在运动的过程中,![]() 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)A(-2,0)、B(0,3);(2)∠APD=90°;(3)∠N的大小不变,∠N=45°
【解析】
(1)利用非负数的和为零,各项分别为零,求出a,b的值;
(2)如图,作DM∥x轴,结合题意可设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,根据平角的定义可知∠OAD=90°-2y,由平行线的性质可得∠OAD+∠ADM=180°,即90-2y+2x+90°=180°,进而可得出x=y,再结合图形即可得出∠APD的度数;
(3)∠N的大小不变,∠N=45°,如图,过D作DE∥BC,过N作NF∥BC,根据平行线的性质可知∠BMD+∠OAD=∠ADM=90°,然后根据角平分线的定义和平行线的性质,可得∠ANM=![]() ∠BMD+
∠BMD+![]() ∠OAD,据此即可得到结论.
∠OAD,据此即可得到结论.
(1)由![]() ,可得
,可得![]() 和
和![]() ,
,
解得![]()
∴A的坐标是(-2,0)、B的坐标是(0,3);
(2)如图,作DM∥x轴
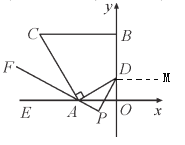
根据题意,设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,
∵∠CAD=90°,
∴∠CAE+∠OAD=90°,
∴2y+∠OAD=90°,
∴∠OAD=90°-2y,
∵DM∥x轴,
∴∠OAD+∠ADM=180°,
∴90-2y+2x+90°=180°,
∴x=y,
∴∠APD=180°-(∠PAD+∠ADP)=180°-(y+90°-2y+x)=180°-90°=90°
(3)∠N的大小不变,∠N=45°
理由:如图,过D作DE∥BC,过N作NF∥BC.
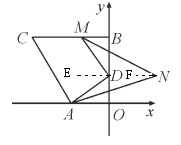
∵BC∥x轴,
∴DE∥BC∥x轴,NF∥BC∥x轴,
∴∠EDM=∠BMD,∠EDA=∠OAD,
∵DM⊥AD,
∴∠ADM=90°,
∴∠BMD+∠OAD=∠EDM+∠EDA=∠ADM=90°,
∵MN平分∠BMD,AN平分∠DAO,
∴∠BMN=![]() ∠BMD,∠OAN=
∠BMD,∠OAN=![]() ∠OAD,
∠OAD,
∴∠ANM=∠BMN+∠OAN=![]() ∠BMD+
∠BMD+![]() ∠OAD
∠OAD
=![]() ×90°=45°.
×90°=45°.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】为了帮助湖北省武汉市防控新冠肺炎,某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物资共2000件送往灾区,已知每件甲种物资的价格比每件乙种物资的价格贵10元,用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同.
(1)求甲、乙两种救灾物资每件的价格各是多少元?
(2)经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,若该爱心组织如何购买这2000件物资,才能使得购买资金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是 ;(精确到0.01)
(2)估算袋中白球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
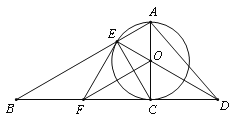
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE
(2)求证:EF是⊙O的切线;
(3)若![]() O的半径为3,∠EAC=60°,求AD的长.
O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且![]() =
=![]() .连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
.连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .其中正确的是________.
.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种竹制躺椅如图①所示,其侧面示意图如图②③所示,这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度.假设AB所在的直线为地面,已知AE=120 cm,当把图②中的支撑杆CD调节至图③中的C′D的位置时,∠EAB由20°变为25°.
(1)你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗?(结果精确到0.1 cm,参考数据:sin 20°≈0.342 0,sin 25°≈0.422 6)
(2)已知点O为AE的一个三等分点,根据人体工程学,当点O到地面的距离为26 cm时,人体感觉最舒适.请你求出此时枕部E到地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
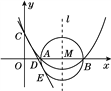
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
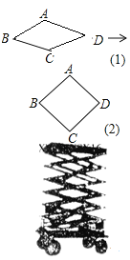
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com