
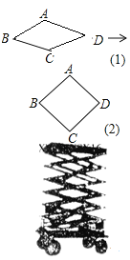
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
【答案】(1)AC=1米,整个装修平台的高度为6米 ;(2)整个装修平台升高了![]() 米
米
【解析】
(1)连接图(1)中菱形ABCD的对角线AC、BD,交于O,则利用菱形的对角线互相垂直可得出对角线AC的长度,继而可得出整个平台的高度.
(2)结合(1)的求解方法可求出此时的平台高度,两者相减即可得出答案.
解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,
在Rt![]() ABO中,∠AOB=90°,∠ABO=
ABO中,∠AOB=90°,∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
∴OA=ABsin∠ABO=1×sin30°=0.5,
此时AC=2AO=2×0.5=1(米),
故可得整个装修平台的高度=1×6=6(米);
(2)当∠ABC从60°变为90°时,AC=![]() ,
,
此时的整个装修平台的高度=![]() ×6≈1.41×6≈8.46,
×6≈1.41×6≈8.46,
整个装修平台升高的高度为8.46﹣6=2.46≈2.5米.



科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
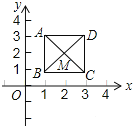
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 点是第二象限内一点,
点是第二象限内一点,![]() 轴于
轴于![]() ,且
,且![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() 是x轴负半
是x轴负半![]() 轴上一点,且
轴上一点,且![]() .
.

(1)![]() ( ),
( ),![]() ( )
( )
(2)如图2,设![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,
时,![]() 的角平分线与
的角平分线与![]() 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点![]() ,求
,求![]() 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为![]() )
)
(3)如图3,当![]() 点在线段
点在线段![]() 上运动时,作
上运动时,作![]() 交
交![]() 于
于![]() 的平分线交于
的平分线交于![]() ,当
,当![]() 点在运动的过程中,
点在运动的过程中,![]() 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
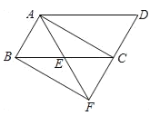
【题目】已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,判断四边形ABFC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
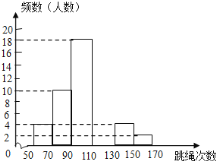
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号中:8,﹣![]() ,+2.8,π,
,+2.8,π,![]() ,﹣0.003,0,﹣100,﹣3.626626662……
,﹣0.003,0,﹣100,﹣3.626626662……
正数集合{_____ …}
整数集合{_____…}
负分数集合{_____ …}
无理数集合{_____ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com