
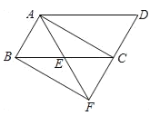
【题目】已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,判断四边形ABFC的形状,并说明理由.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】周日上午小明从家跑步去图书馆,在那里看了一会儿书后又走到文具店去买笔记本,然后散步回家.下图反映的是小明离家的距离![]() 与所用时间
与所用时间![]() 之间的函数关系,据此回答问题:
之间的函数关系,据此回答问题:
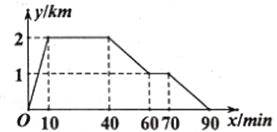
(1)图书馆离小明家 ![]() ,小明从家到图书馆用了
,小明从家到图书馆用了 ![]() .
.
(2)图书馆离文具店____![]() .
.
(3)小明在文具店停留了 ![]()
(4)小明从文具店回到家的平均速度是多少千米/小时?(写出简要计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
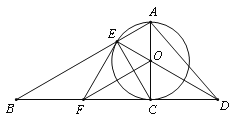
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.
(1)求证:OF⊥CE
(2)求证:EF是⊙O的切线;
(3)若![]() O的半径为3,∠EAC=60°,求AD的长.
O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种竹制躺椅如图①所示,其侧面示意图如图②③所示,这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度.假设AB所在的直线为地面,已知AE=120 cm,当把图②中的支撑杆CD调节至图③中的C′D的位置时,∠EAB由20°变为25°.
(1)你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗?(结果精确到0.1 cm,参考数据:sin 20°≈0.342 0,sin 25°≈0.422 6)
(2)已知点O为AE的一个三等分点,根据人体工程学,当点O到地面的距离为26 cm时,人体感觉最舒适.请你求出此时枕部E到地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
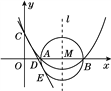
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
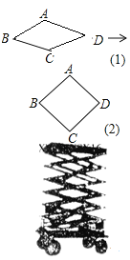
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今秋,河北保定易县柿子虽大丰收,却让果农犯了愁.据悉,今年易县有2亿斤柿子滞销,少数乡镇柿子只得4毛钱贱卖,多地柿子无人问津,为解决销路,一家柿子种植大户为村里联系了一个销售渠道,已知有480吨的柿子需运出,某汽车运输公司承办了这次运送任务.
(1)运输公司平均每天运送柿子x吨,需要y天完成运输任务,写出y关于x的函数解析式;
(2)这个公司计划派出4辆卡车,每天共运送32吨.
①求需要多少天完成全部运送任务?
②现需要提前5天运送完毕,需增派同样的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
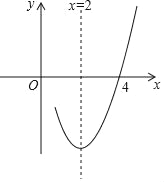
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com