练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知正方形ABCD，对角线的交点M（2，2）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（　　）

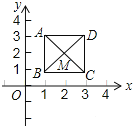
    A. （﹣2012，2）B. （﹣2012，﹣2）C. （﹣2013，﹣2）D. （﹣2013，2）

    【答案】A

    【解析】

    根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标，即可得规律：第n次变换后的点M的对应点的为：当n为奇数时为（2﹣n，﹣2），当n为偶数时为（2﹣n，2），继而求得结果．

    解：∵对角线交点M的坐标为（2，2），

    根据题意得：第1次变换后的点M的对应点的坐标为（2﹣1，﹣2），即（1，﹣2），

    第2次变换后的点M的对应点的坐标为：（2﹣2，2），即（0，2），

    第3次变换后的点M的对应点的坐标为（2﹣3，﹣2），即（﹣1，﹣2），

    第n次变换后的点M的对应点的为：当n为奇数时为（2﹣n，﹣2），当n为偶数时为（2﹣n，2），

    ∴连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（﹣2012，2）．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AB＝3，BC＝10，∠A＝45°，点E是边AD上一动点，将△AEB沿直线BE折叠，得到△FEB，设BF与AD交于点M，当BF与ABCD的一边垂直时，DM的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了帮助湖北省武汉市防控新冠肺炎，某爱心组织筹集了部分资金，计划购买甲、乙两种救灾物资共2000件送往灾区，已知每件甲种物资的价格比每件乙种物资的价格贵10元，用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同．

    （1）求甲、乙两种救灾物资每件的价格各是多少元?

    （2）经调查，灾区对甲种物资的需求量不少于乙种物资的1.5倍，若该爱心组织如何购买这2000件物资，才能使得购买资金最少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周日上午小明从家跑步去图书馆，在那里看了一会儿书后又走到文具店去买笔记本，然后散步回家.下图反映的是小明离家的距离 与所用时间之间的函数关系，据此回答问题：

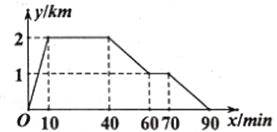
    (1)图书馆离小明家 ，小明从家到图书馆用了 ．

    (2)图书馆离文具店____．

    (3)小明在文具店停留了

    (4)小明从文具店回到家的平均速度是多少千米/小时?(写出简要计算过程)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

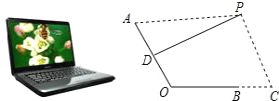
    【题目】如图是一台放置在水平桌面上的笔记本电脑，将其侧面抽象成如右图所示的几何图形，若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm，点P为眼睛所在位置，D为AO的中点，连接PD，当PD?AO时，称点P为“最佳视角点”，作PC?BC，垂足C在OB的延长线上，且BC=12cm．

    （1）当PA=45cm时，求PC的长；

    （2）若?AOC=120°时，“最佳视角点”P在直线PC上的位置会发生什么变化？此时PC的长是多少？请通过计算说明．（结果精确到0.1cm，可用科学计算器，参考数据： ， ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC内接于⊙O，P是上任一点（点P不与点A、B重合），连AP、BP，过点C作CM∥BP交PA的延长线于点M．

    （1）填空：∠APC＝____ 度，∠BPC＝____度；

    （2）求证：△ACM≌△BCP；

    （3）若PA＝1，PB＝2，求梯形PBCM的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．

    摸球的次数n

    100

    150

    200

    500

    800

    1000

    摸到黑球的次数m

    23

    31

    60

    130

    203

    251

    摸到黑球的频率

    0.23

    0.21

    0.30

    0.26

    0.253

    （1）补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是　 　；（精确到0.01）

    （2）估算袋中白球的个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

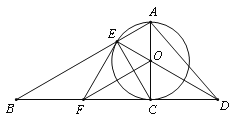
    【题目】已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，作OF∥AB交BC于点F，连接EF．

    （1）求证：OF⊥CE

    （2）求证：EF是⊙O的切线；

    （3）若O的半径为3，∠EAC＝60°，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

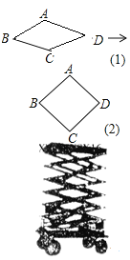
    【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台，其基本图形是菱形，主体部分相当于由6个菱形相互连接而成，通过改变菱形的角度，从而可改变装修平台高度．

    （1）如图（1）是一个基本图形，已知AB=1米，当∠ABC为60°时，求AC的长及此时整个装修平台的高度（装修平台的基脚高度忽略不计）；

    （2）当∠ABC从60°变为90°（如图（2）是一个基本图形变化后的图形）时，求整个装修平台升高了多少米．[结果精确到0.1米］

    查看答案和解析>>

    同步练习册答案