
【题目】如图,等边△ABC内接于⊙O,P是![]() 上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC=____ 度,∠BPC=____度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积.

【答案】(1)∠APC=60°,∠BPC=60°;(2)证明见解析;(3)![]()
【解析】试题分析:(1)同弧所对圆周角相等.(2)证明A、P、B、C四点共圆,再利用AAS证明三角形全等.(3) 作PH⊥CM于H,利用(2)全等证明![]() PCM是等边三角形,Rt△PMH是30°特殊三角形,可求得梯形PBCM的面积.
PCM是等边三角形,Rt△PMH是30°特殊三角形,可求得梯形PBCM的面积.
试题解析:
解答:(1)解:∠APC=60°,∠BPC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°-∠BPM=180°-(∠APC+∠BPC)=180°-120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°,
∴∠MAC=∠PBC,
∵AC=BC,
∴△ACM≌△BCP;
(3)解:作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+PB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=![]() ,
,
∴S梯形PBCM=![]() (PB+CM)×PH=
(PB+CM)×PH=![]() (2+3)×
(2+3)×![]() =
= ![]() .
.


科目:初中数学 来源: 题型:
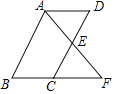
【题目】如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若AB=8,BC=5,则EF的长为 时,AB⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的顶点A,B分别在y轴和x轴上,边CD交x轴的正半轴于点E.
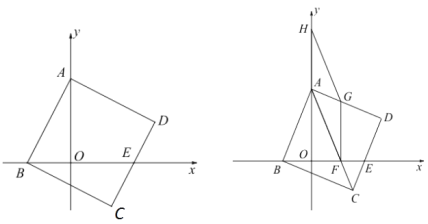
(1)若A(0,a),且![]() ,求A点的坐标;
,求A点的坐标;
(2)在(l)的条件下,若3AO=4EO,求D点的坐标;
(3)如图2,连结AC交x轴于点F,点H是A点上方y轴上一动点,以AF、AH为边作平行四边形AFGH,使G点恰好落在AD边上,试探讨BF,HG与DG的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究一次函数![]() 的图像性质时我们有如下发现:
的图像性质时我们有如下发现:
①系数![]() 决定了函数图像的坡度,
决定了函数图像的坡度,![]() 越大则图像坡度越大(越靠近
越大则图像坡度越大(越靠近![]() 轴),
轴),![]() 越小则图像坡度越小(越靠近
越小则图像坡度越小(越靠近![]() 轴);
轴);
②常数项![]() 决定了图像与
决定了图像与![]() 轴的交点,即函数图像与
轴的交点,即函数图像与![]() 轴交点坐标始终为
轴交点坐标始终为![]() .
.
基于以上发现,我们得出结论:如果两个一次函数的![]() 值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的
值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的![]() 值一定相等:把函数图像沿
值一定相等:把函数图像沿![]() 轴向上(或向下) 平移
轴向上(或向下) 平移![]() 个单位, 系数
个单位, 系数![]() 保持不变, 常数
保持不变, 常数![]() 变为
变为![]() (或
(或![]() ).如:函数
).如:函数![]() 和
和![]() 的图像互相平行:函数
的图像互相平行:函数![]() 的图像向上平移2个单位后所得函数表达式为
的图像向上平移2个单位后所得函数表达式为![]() .
.
据此回答下列问题:
(1) 把函数![]() 的图像向上平移4个单位后所得函数的表达式为____;
的图像向上平移4个单位后所得函数的表达式为____;
(2)把函数![]() 的图像向 (上或下)平移 个单位可得到函数
的图像向 (上或下)平移 个单位可得到函数![]() 的图像;
的图像;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,求出直线
平行,求出直线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
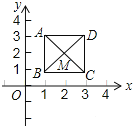
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A、B两点.
![]()
(1)分别写出A、B两点表示的数: 、 ;
(2)若点C表示﹣0.5,把点C表示在如图所示的数轴上;
(3)将点B向左移动3个单位长度,得到点D,点A、B、C、D所表示的四个数用“<”连接的结果: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AF=BD.
(2)求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
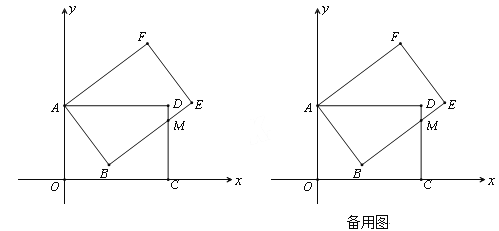
【题目】矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
(1)求AD的长;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在直线AM下方,(2)中的抛物线上是否存在点P,使S△PAM =![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com