
【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
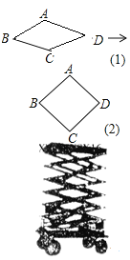
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
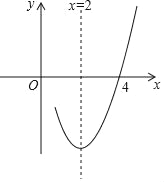
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
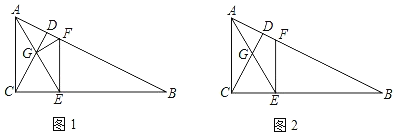
【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
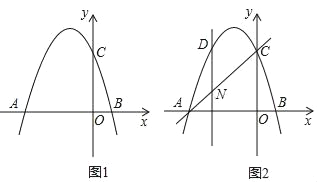
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恒昌路是一条东西走向的马路,有市场、医院、车站、学校四家公共场所。已知市场在医院东200米,车站在市场东150米,医院在学校东450米。若将马路近似的看成一条直线,以医院为原点,向东方向为正方向,用1个单位长度表示100米,
(1)在数轴上表示出四家公共场所的位置;
![]()
(2)列式计算学校与车站之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
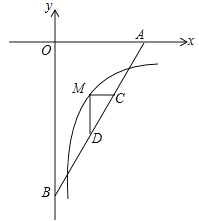
【题目】(2017湖北省十堰市,第10题,3分)如图,直线![]() 分别交x轴,y轴于A,B,M是反比例函数
分别交x轴,y轴于A,B,M是反比例函数![]() (x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=
(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=![]() ,则k的值为( )
,则k的值为( )
A. ﹣3 B. ﹣4 C. ﹣5 D. ﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com