
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.
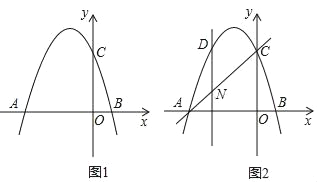
【答案】(1)y=﹣x2﹣x+2; (2)(0,2)或(﹣1,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2);(3)1.
,﹣2);(3)1.
【解析】(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;
(2)设M点坐标为(m,n),根据S△AOM=2S△BOC列出关于m的方程,解方程求出m的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式为y=x+2,再设N点坐标为(x,x+2),则D点坐标为(x,-x2-x+2),然后用含x的代数式表示ND,根据二次函数的性质即可求出线段ND长度的最大值.
解:(1)A(﹣2,0),C(0,2)代入抛物线的解析式y=﹣x2+mx+n,
得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2﹣x+2.
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣x+2,则易得B(1,0),设M(m,n)然后依据S△AOM=2S△BOC列方程可得:
![]() AO×|n|=2×
AO×|n|=2×![]() ×OB×OC,
×OB×OC,
∴![]() ×2×|﹣m2﹣m+2|=2,
×2×|﹣m2﹣m+2|=2,
∴m2+m=0或m2+m﹣4=0,
解得m=0或﹣1或![]() ,
,
∴符合条件的点M的坐标为:(0,2)或(﹣1,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).
(3)设直线AC的解析式为y=kx+b,将A(﹣2,0),C(0,2)代入
得到![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=x+2,
设N(x,x+2)(﹣2≤x≤0),则D(x,﹣x2﹣x+2),
ND=(﹣x2﹣x+2)﹣(x+2)=﹣x2﹣2x=﹣(x+1)2+1,
∵﹣1<0,
∴x=﹣1时,ND有最大值1.
∴ND的最大值为1.


科目:初中数学 来源: 题型:
【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的个数有( )
①绝对值小于π的整数有7个
②正整数和负整数统称为整数
③一个数的绝对值等于本身的数是正数
④异号两数相加的和一定小于每一个加数
⑤倒数等于本身的数是1和0
⑥若干个有理数相乘积为负数,则正因数的个数应为奇数个.
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
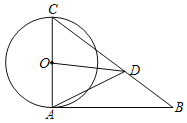
【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=![]() ,求tan∠ADO.
,求tan∠ADO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是最大的负整数,b是最小的正整数,且c=a+b,请回答下列问题:
![]()
(1)请直接写出a,b,c的值:a= ;b= ;c= ;
(2)a,b,c在数轴上所对应的点分别为A,B,C,请在如图的数轴上表示出A,B,C三点;
(3)在(2)的情况下.点A,B,C开始在数轴上运动,若点A,点C以每秒1个单位的速度向左运动,同时,点B以每秒5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出AB﹣BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
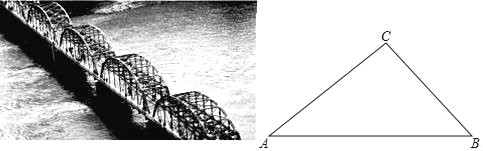
【题目】汾河孕育着世代的龙城子孙,而魅力汾河两岸那“新外滩”的称号,将太原人对汾河的爱表露无遗…贯穿太原的汾河,让桥,也成为太原的文化符号,让汾河两岸,也成为繁华的必争之地!北中环桥是世界上首座对称五拱反对称五跨非对称斜拉索桥,2013年开工建设,当年实现全线竣工通车.这座桥造型现代,宛如一条腾飞巨龙.
小芸和小刚分别在桥面上的A,B处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
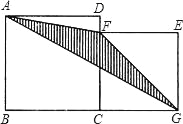
【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
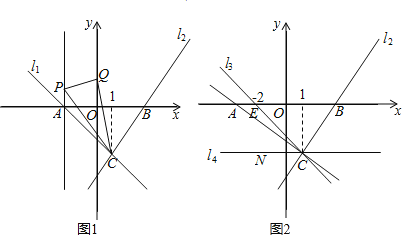
【题目】已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=![]() x﹣
x﹣![]() 与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
(1)如图,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;
(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;
(3)如图,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形,若存在, 求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com