Question

【题目】已知直线l1：y＝﹣x+b与x轴交于点A，直线l2：y＝x﹣与x轴交于点B，直线l1、l2交与点C，且C点的横坐标为1．

（1）如图，过点A作x轴的垂线，若点P（x，2）为垂线上的一个点，Q是y轴上一动点，若S△CPQ＝5，求此时点Q的坐标；

（2）若P在过A作x轴的垂线上，点Q为y轴上的一个动点，当CP+PQ+QA的值最小时，求此时P的坐标；

（3）如图，点E的坐标为（﹣2，0），将直线l1绕点C旋转，使旋转后的直线l3刚好过点E，过点C作平行于x轴的直线l4，点M、N分别为直线l3、l4上的两个动点，是否存在点M、N，使得△BMN是以M点为直角顶点的等腰直角三角形，若存在， 求出N点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）Q的坐标为（0,0）或（0，-5）；（2）点P的坐标为（﹣3，﹣）；（3）①点N的坐标为（﹣16，﹣4），②点N的坐标为（﹣，﹣4）或（﹣16，﹣4）．

【解析】

（1）当x=1时，y=x﹣，即点C的坐标为（1，-4），将点C的坐标代入直线l1：y=-x+b中，即可求直线l1解析式；再根据P点纵坐标为2，求出P点坐标，然后求出直线AC的解析式，因为直线AC交y轴于点M，所以M横坐标为0，再求出纵坐标，最后根据S△CPQ＝QM×（xC﹣xP）＝=5，解得：yQ=0或-5，即可得出结果；（2）根据最短路径问题可得：作C关于过A垂线的对称点C′（﹣7，﹣4）、A关于y轴的对称点A′（3，0），连接A′C′交过A点的垂线与点P，交y轴于点Q，此时，CP+PQ+QA的值最小，解得直线A′C′的表达式，从而求得点P的坐标；（3）如图2，点E的坐标为（-2，0），将直线l1绕点C逆时针旋转，使旋转后的直线l3刚好过点E，过点C作平行于x轴的直线l4，点M、N分别为直线l3、l4上的两个动点，是否存在点M、N，使得△BMN是以M点为直角顶点的等腰直角三角形，若存在，直接写出N点的坐标；若不存在，请说明理由．

（1）直线l2：y＝x﹣，令x＝1，则y＝﹣4，故C（1，﹣4），

把C（1，﹣4）代入直线l1：y＝﹣x+b，得：b＝﹣3，则l1为：y＝﹣x﹣3， 所以A（﹣3，0），所以点P坐标为（﹣3，2），如图，设直线AC交y轴于点M，

设yPC＝mx+t得：，解得， ∴yPC＝-1.5x-2.5，即M（0，-2.5）．

S△CPQ＝QM×（xC﹣xP）＝=5，解得：yQ=0或-5，

∴Q的坐标为（0,0）或（0，）

（2）确定C关于过A垂线的对称点C′（﹣7，﹣4）、A关于y轴的对称点A′（3，0），

连接A′C′交过A点的垂线与点P，交y轴于点Q，此时，CP+PQ+QA的值最小，

将点A′、C′点的坐标代入一次函数表达式：y＝k′x+b′得：，解得： ，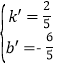

则直线A′C′的表达式为：y＝x﹣，当x＝﹣3时，y＝﹣，

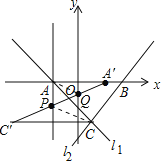
即点P的坐标为（﹣3，﹣），

（3）将E、C点坐标代入一次函数表达式，同理可得其表达式为

①当点M在直线l4上方时，设点N（n，﹣4），点M（s，﹣s﹣），点B（4，0），

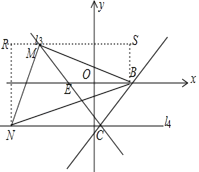
过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S，

∵∠RMN+∠RNM＝90°，∠RMN+∠SMR＝90°，

∴∠SMR＝∠RNM，

∠MRN＝∠MSB＝90°，MN＝MB，

∴△MSB≌△NRM（AAS），

∴RN＝MS，RM＝SB，

即 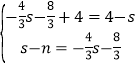，解得

故点N的坐标为（﹣16，﹣4），

②当点M在l4下方时，如图1，过点M作PQ∥x轴，与过点B作y轴的平行线交于Q，与过点N作y轴的平行线交于P，

同①的方法得，N（﹣，﹣4），

即：点N的坐标为（﹣，﹣4）或（﹣16，﹣4）．