
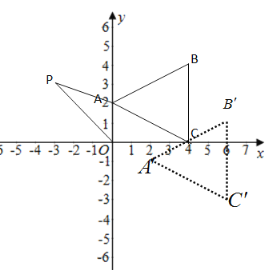
【题目】如图,△ABC在直角坐标系中,

(1)若把△ABC向右平移2个单位,再向下平移3个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(2)如果在第二象限内有一点P(m,3),四边形ACOP的面积为 (用含m的式子表示)
(3)在(2)的条件下,是否存在点P,使四边形ACOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)A′(2,-1)、B′(6,1)、C′(6,-3),见解析;(2)S四边形ABOP=4﹣m;(3)存在,点P(﹣4,3)使S四边形ABOP=S△ABC.
【解析】
(1)利用平移的性质,描出A、B、C平移后的点,再顺次连接即可;
(2)S四边形ACOP=S△ACO+S△APO,利用各点的坐标以及三角形的面积公式即可求得;
(3)求出S△ABC的面积,再利用S四边形ACOP=S△ABC即可求出m的值,即可得出点P的坐标.
解:(1)平移得到△![]() 如图所示
如图所示
A′(2,-1)、B′(6,1)、C′(6,-3)
(2)四边形ACOP的面积为 (4-m)
∵S△ACO=![]() ×2×4=4,S△APO=
×2×4=4,S△APO=![]() ×2×(﹣m)=﹣m,
×2×(﹣m)=﹣m,
∴S四边形ACOP=S△ACO+S△APO=4+(﹣m)=4﹣m,
即S四边形ACOP=4﹣m;
(3)因为S△ABC=![]() ×4×4=8,
×4×4=8,
∵S四边形ACOP=S△ABC
∴4﹣m=8,
则 m=﹣4,
所以存在点P(﹣4,3)使S四边形ACOP=S△ABC.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
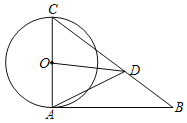
【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=![]() ,求tan∠ADO.
,求tan∠ADO.
查看答案和解析>>
科目:初中数学 来源: 题型:
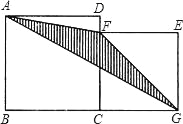
【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
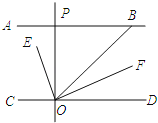
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有_____填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
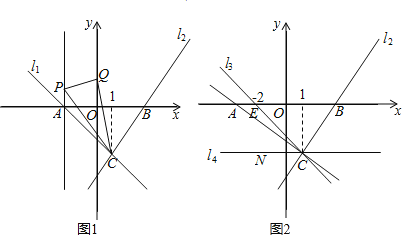
【题目】已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=![]() x﹣
x﹣![]() 与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
(1)如图,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;
(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;
(3)如图,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形,若存在, 求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2![]() =2×
=2×![]() +1,5
+1,5![]() =5×
=5×![]() +1,给出定义如下:我们称使等式ab=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式ab=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(2,1),(3,![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(a,3)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则(n,m)“共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的“共生有理数对”为(注意:不能与题目中已有的“共生有理数对”重复).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com