
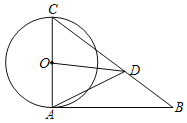
【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=![]() ,求tan∠ADO.
,求tan∠ADO.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设线段AD与⊙O交于E,连接CE,根据AC为⊙O的直径,可得CE⊥AD,再根据等腰三角形三线合一的性质可得∠ACD=2∠ACE,根据∠ACB=2∠BAD,从而得出∠ACE=∠DAB,再根据∠CAE=90°,可推出∠CAB=90°,即可证明AB与⊙O相切;
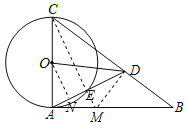
(2)延长CE交AB于M,则CM为AD的垂直平分线,连接DM,通过证明△ACM≌△DCM(SSS),可得∠BDM=90°,再根据锐角三角函数和中位线的性质求解即可.
(1)证明:设线段AD与⊙O交于E,连接CE,
∵AC为⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴∠ACD=2∠ACE,
∵∠ACB=2∠BAD,
∴∠ACE=∠DAB,
∵∠CAE=90°,
∴∠CAE+∠DAB=90,
∴∠CAB=90°,
∴AB与⊙O相切;
(2)解:∵AB与⊙O相切,
∴∠CAB=90°,
延长CE交AB于M,则CM为AD的垂直平分线,连接DM,
∴DM=AM,
∵AC=CD,CM=CM,
∴△ACM≌△DCM(SSS),
∴∠CDM=∠CAB=90°,
∴∠BDM=90°,
∵tanB=![]() ,
,
∴设AM=MD=3a,DB=4a,MB=5a,
AB=8a,AC=6a,
∴tan∠ACM=tan∠EAM=![]() ,
,
∴CE=2AE,AE=2EM,
设EN=k,
∴AE=DE=2k,CE=4k,
过O作ON⊥AD于N,
∴ON∥CE,
∴ON=![]() CE=2k,AN=
CE=2k,AN=![]() AE=k,
AE=k,
∴DN=3AN=3k,
∴tan∠ADO=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
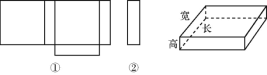
【题目】小明在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了几条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:已知这个长方体纸盒高为20 cm,底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
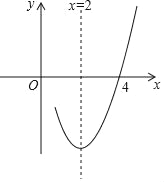
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
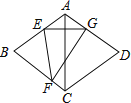
【题目】如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,将菱形沿EF折叠,点B恰好落在AD边上的点G处,且EG⊥AC,若CD=8,则FG的长为( )
A. 6B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
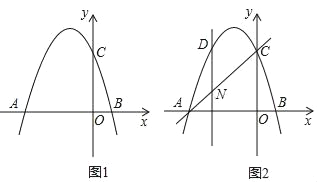
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)若把△ABC向右平移2个单位,再向下平移3个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(2)如果在第二象限内有一点P(m,3),四边形ACOP的面积为 (用含m的式子表示)
(3)在(2)的条件下,是否存在点P,使四边形ACOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com