【题目】如图，等腰直角三角形
中，
，
.先将
绕点
逆时针方向旋转
，得到
，点
对应点
，点
对应点
；再将沿
方向平移，得到
，点、、的对应点分别是点
、
、
，设平移的距离为
，且
．
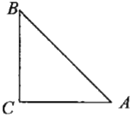
（1）在图中画出和；
（2）记
与
的交点为点
，
与
的交点为点
，如果四边形
的面积是
的面积的3倍，试求四边形
和
的面积的比值．
【答案】（1）见解析 （2）3
【解析】
（1）根据作法将AB、AC分别逆时针旋转90°可得AB1、AC1，连接B1C1即可得
；将沿
方向平移，得到
，因为平移的距离为
，且
，故要注意C2在线段C1A上；
（2）根据旋转的性质先证四边形AC1B1C是正方形，再根据四边形
的面积是
的面积的3倍求得D为AC的中点，利用三角形是全等进行转化即可．
（1）如图，和就是所求的三角形．
（2）连接B1C，如图：
由题意可得：∠CAC1=∠C1=90°，CB=CA=C1A=C1B1
∴AC∥B1C1
∴四边形AC B1C1是平行四边形
又∠C1=90°，CA=C1A
∴四边形AC B1C1是正方形
∴
90°
∴B1、C、B三点共线，B1C∥AC1
∴B2在B1C上
∵四边形的面积是的面积的3倍
∴四边形AC B2C2的面积是的面积的4倍
即
∴AC=2CD，AD=CD
又
90°，
∴
∴
∴矩形
的面积=矩形
的面积
又
90°，
∴
∴
的面积是四边形AC B2C2的面积的
，即为矩形的面积的
∴四边形
是的面积的3倍
∴四边形和的面积的比值为3 ．
天天练口算系列答案科目：初中数学 来源： 题型：
【题目】某校对九年级全体学生进行了一次学业水平测试，成绩评定分为A，B，C，D四个等级（A，B，C，D分别代表优秀、良好、合格、不合格）该校从九年级学生中随机抽取了一部分学生的成绩，绘制成以下不完整的统计图．请你根据统计图提供的信息解答下列问题；
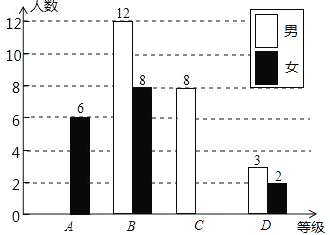
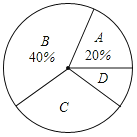
（1）本次调查中，一共抽取了 名学生的成绩；
（2）将上面的条形统计图补充完整，写出扇形统计图中等级C的百分比 ．
（3）若等级D的5名学生的成绩（单位：分）分别是55、48、57、51、55．则这5个数据的中位数是 分，众数是 分．
（4）如果该校九年级共有500名学生，试估计在这次测试中成绩达到优秀的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
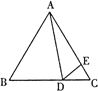
【题目】如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且 ∠ADE=60°，BD=4，CE=
，则△ABC的面积 为（ ）
A. 
B. 15 C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
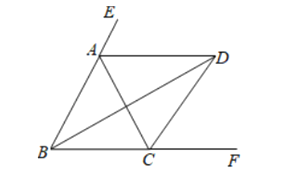
【题目】如图，
， AD、BD、CD分别平分
外角
、内角
、外角
.以下结论:①
:②
；③
；④
:⑤
.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】)6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成如下统计图：
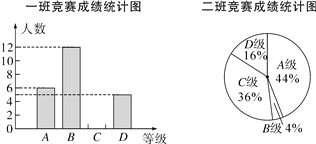
根据以上提供的信息解答下列问题：
(1)把一班竞赛成绩统计图补充完整；
(2)写出下表中a，b，c的值：
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析：
①从平均数和中位数方面比较一班和二班的成绩；
②从平均数和众数方面比较一班和二班的成绩；
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l有上三点M，O，N，MO=3，ON=1；点P为直线l上任意一点，如图画数轴．
（1）当以点O为数轴的原点时，点P表示的数为x，且点P到点M、点N的距离相等，那么x的值是________；
（2）当以点M为数轴的原点时，点P表示的数为y，当y= 时，使点P到点M、点N 的距离之和是5；
（3）若以点O为数轴的原点，点P以每秒2个单位长度的速度从点O向左运动时，点E从点M以每秒1个单位长度速度向左运动，点F从点N每秒3个单位长度的向左运动，且三点同时出发，求运动几秒时点P、点E、点F表示的数之和为-20．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
关于x的方程：
的解是
，
；
即
的解是
；
的解是，
；
的解是，
；
请观察上述方程与解的特征，比较关于x的方程
与它们的关系，猜想它的解是什么？并利用“方程的解”的概念进行验证．
由上述的观察、比较、猜想、验证，可以得出结论：
如果方程的左边是未知数与其倒数的倍数的和，方程的右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解关于x的方程：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=
x+
与x轴交于点A，与y轴交于点C，以AC为直径作⊙M，点D是劣弧AO上一动点（D点与A，C不重合）．抛物线y=－x+bx+c经过点A、C，与x轴交于另一点B，
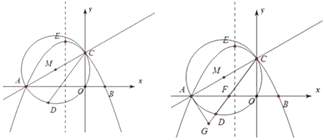
（1）求抛物线的解析式及点B的坐标；
（2）在抛物线的对称轴上是否存在一点P，是︱PA—PC︱的值最大；若存在，求出点P的坐标；若不存在，请说明理由。
（3）连CD交AO于点F，延长CD至G，使FG=2，试探究当点D运动到何处时，直线GA与⊙M相切，并请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，四边形
是矩形，点
，点
，点
.以点
为中心，顺时针旋转矩形，得到矩形
，点
，
，
的对应点分别为
，
，
.
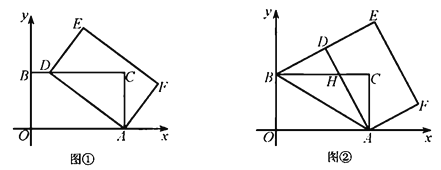
（Ⅰ）如图①，当点落在
边上时，求点的坐标；
（Ⅱ）如图②，当点落在线段
上时，
与交于点
.
①求证
；
②求点的坐标.
（Ⅲ）记
为矩形对角线的交点，
为
的面积，求的取值范围（直接写出结果即可）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com