
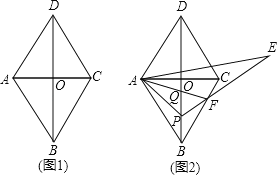
【题目】如图,在菱形ABCD中,边长为2![]() ,∠BAD=120°,点P从点B开始,沿着B→D方向,速度为每秒1个单位,运动到点D停止,设运动的时间为t(秒),将线段AP绕点A逆时针旋转60°,得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E,
,∠BAD=120°,点P从点B开始,沿着B→D方向,速度为每秒1个单位,运动到点D停止,设运动的时间为t(秒),将线段AP绕点A逆时针旋转60°,得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E,
(1)当t=0时,求AE的值.
(2)P点在运动过程中,线段PE与菱形的边框交于点F.(精确到0.1)
问题1:如图2,当∠BAP=11°,AF=2PF,则OQ= .
问题2:当t为何值时,△APF是含有30°角的直角三角形,写出所有符合条件的t的值 .
(![]() ≈1.73,sin11°≈0.19,cos11°≈0.98,sin19°≈0.33,tan19°≈0.34,sin41°≈0.65,tan41°≈0.87)
≈1.73,sin11°≈0.19,cos11°≈0.98,sin19°≈0.33,tan19°≈0.34,sin41°≈0.65,tan41°≈0.87)
(3)当点P在运动过程中,求出△ACE的面积y关于时间t的函数表达式.(请说明理由)
【答案】(1)AE=4![]() ;(2)问题1:OQ≈0.6,问题2:t=1s或4s时,∠PAF=30°;(3)S△ACE=
;(2)问题1:OQ≈0.6,问题2:t=1s或4s时,∠PAF=30°;(3)S△ACE=![]() t(0<t≤6)..
t(0<t≤6)..
【解析】
(1)利用直角三角形30度角的性质解决问题即可.
(2)①根据OQ=OAtan19°,求出OA即可解决问题.
②分两种情形:如图2-2中,当∠PAF=30°时,延长FP到H,使得PH=PF,连接AH,BH.如图2-1中,当∠PAF=30°,分别求解即可.
(3)如图3中,作BM⊥AB交AC的延长线于M,作EH⊥AM于H,连接EM.证明△EAM∽△PAB,推出![]() =2,求出EM即可解决问题.
=2,求出EM即可解决问题.
(1)t=0时,点P与点B重合,
∵∠PAE=60°,∠APE=60°,
∴∠E=30°,
∴AE=2PA=2AB=4![]() .
.
(2)①如图2中,
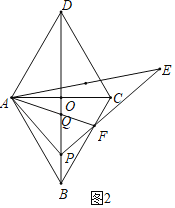
∵四边形ABCD是菱形,∠DAB=120°,
∴∠DAC=∠CAB=60°,AD=CD=AB=BC=2![]() ,
,
∴△ADC,△ABC都是等边三角形,
∴AC=AB=2![]() ,OA=OC=
,OA=OC=![]() ,
,
∵∠APF=90°,
∴sin∠PAF=![]() =
=![]() ,
,
∴∠PAF=30°,
∴∠OAQ=60°﹣11°﹣30°=19°,
∴OQ=OAtan19°≈0.6.
故答案为0.6.
②如图2﹣2中,当∠PAF=30°时,延长FP到H,使得PH=PF,连接AH,BH.
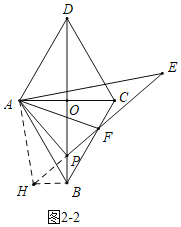
∵PA⊥FH,FP=FH,
∴AF=AH,
∵∠PAF=30°,
∴∠AFH=60°,
∴△AFH是等边三角形,
∴∠PAH=∠PAF=30°,
∴PA=![]() PH,
PH,
∵∠AHF=∠ABC
∴A,H,B,F四点共圆,
∴∠ABH=∠AFH=60°,
∴∠ABH=∠BAC=60°,
∴BH∥AC,
∵BD⊥AC,
∴BD⊥BH,
由△HBP∽△POA,可知:![]() =
=![]() ,
,
∴OA=![]() t,
t,
∴![]() =
=![]() t,
t,
∴t=1.
如图2﹣1中,当∠PAF=30°,易知∠BAP=90°,
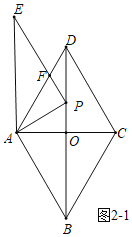
∴PB=![]() =
=![]() =4,
=4,
综上所述,t=1s或4s时,∠PAF=30°.
故答案为1s或4s.
(3)如图3中,作BM⊥AB交AC的延长线于M,作EH⊥AM于H,连接EM.
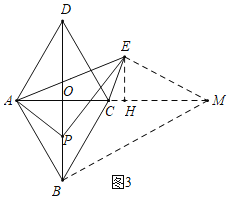
在Rt△ABM中,∵∠ABM=90°,∠BAM=60°,
∴∠AMB=30°,
∴AM=2AB,
在Rt△APE中,∵∠APE=90°,∠PAE=60°,
∴∠AEP=30°,
∴AE=2PA,
∴![]() =
=![]() =2,
=2,
∵∠EAP=∠MAB,
∴∠EAM=∠PAB,
∴△EAM∽△PAB,
∴![]() =
=![]() =2,∠AME=∠ABP=30°,
=2,∠AME=∠ABP=30°,
∴EM=2t,EH=![]() EM=t,
EM=t,
∴S△ACE=![]() ACEH=
ACEH=![]() t(0<t≤6).
t(0<t≤6).


科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.
①请问甲、乙两种物品的单价各为多少?
②如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5050元,通过计算得出共有几种选购方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
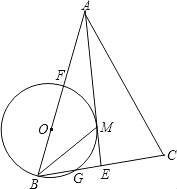
【题目】已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=6,cosC=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com