
分析 如下图所示:∠AOD=∠BOC=60°,即:∠COD=120°>∠AOD=60°,AD是该矩形较短的一边,根据矩形的性质:矩形的对角线相等且互相平分,所以有OA=OD=OC=OB=6,又因为∠AOD=∠BOC=60°,所以AD=OA=0D=6.
解答 解:如下图所示:矩形ABCD,对角线AC=BD=12,∠AOD=∠BOC=60°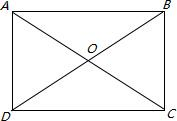 ∵四边形ABCD是矩形
∵四边形ABCD是矩形
∴OA=OD=OC=OB=$\frac{1}{2}$×12=6(矩形的对角线互相平分且相等)
又∵∠AOD=∠BOC=60°,
∴OA=OD=AD=6,
∵∠COD=120°>∠AOD=60°
∴AD<DC
所以该矩形较短的一边长为6,
故答案为:6.
点评 本题主要考查矩形的性质:矩形的对角线相等且互相平分,且矩形对角线相交所的角中“大角对大边,小角对小边”.


科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 2 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
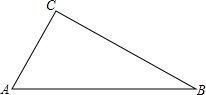 如图,在△ABC中,∠C=90°.
如图,在△ABC中,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
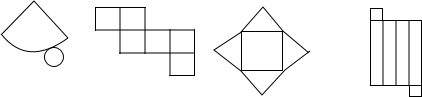
| A. | 圆锥,正方体,四棱锥,四梭柱 | B. | 圆柱,正方体,四棱锥,四梭柱 | ||
| C. | 圆锥,正方体,四棱柱,四梭锥 | D. | 圆柱,正方体,四棱柱,四梭锥 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
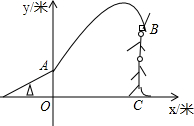 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com