
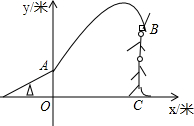
 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.
如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-$\frac{1}{3}$x2+2x+4的一部分.分析 (1)将二次函数化简为y=-$\frac{1}{3}$(x-3)2+7,即可解出y最大的值.
(2)当x=6时代入二次函数可得点B的坐标在抛物线上.
解答 解:(1)将二次函数y=-$\frac{1}{3}$x2+2x+4化成y=-$\frac{1}{3}$(x-3)2+7,
当x=3时,y有最大值,y最大值=7,
因此,演员弹跳离地面的最大高度是7米.
(2)能成功表演.理由是:
当x=6时,y=-$\frac{1}{3}$×62+2×6+4=4.
即点B(6,4)在抛物线y=-$\frac{1}{3}$x2+2x+4上,
因此,能表演成功.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.


科目:初中数学 来源: 题型:解答题
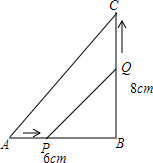 如图,在△ABC中,∠B=90°,点P从A点开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?
如图,在△ABC中,∠B=90°,点P从A点开始沿AB边向B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
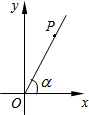 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )
如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com