
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
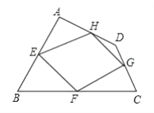
(1)四边形EFGH的形状是_________,证明你的结论;
(2)当四边形 ABCD的对角线满足_________条件时,四边形 EFGH是矩形;你学过的哪种特殊四边形的中点四边形是矩形? ________
(3)当四边形 ABCD的对角线满足_________条件时,四边形 EFGH是菱形;你学过
的哪种特殊四边形的中点四边形是菱形? _________.
【答案】(1) 平行四边形;证明见解析;(2) AC⊥BD, 菱形;(3) AC=BD, 矩形
【解析】试题分析:(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG═
BD,FG∥BD,FG═![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答;
(3)添加的条件应为:AC=BD,把AC=BD作为已知条件,根据三角形的中位线定理可得,HG平行且等于AC的一半,EF平行且等于AC的一半,根据等量代换和平行于同一条直线的两直线平行,得到HG和EF平行且相等,所以EFGH为平行四边形,又EH等于BD的一半且AC=BD,所以得到所证四边形的邻边EH与HG相等,所以四边形EFGH为菱形.根据三角形的中位线定理和矩形的性质得出EF=FG=GH=EH即可得出结论;
试题解析:
(1)四边形EFGH的形状是平行四边形.理由如下:
连结BD,如图所示:
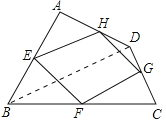
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
连结AC、BD,如图所示:
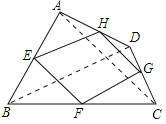
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
菱形的中点四边形是矩形.理由如下:
连结AC、BD,如图所示:
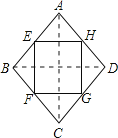
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]()
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形;
(3)添加的条件应为:AC=BD.
证明:∵E,F,G,H分别是边AB、BC、CD、DA的中点,
∴在△ADC中,HG为△ADC的中位线,所以HG∥AC且HG=![]() AC;同理EF∥AC且EF=
AC;同理EF∥AC且EF=![]() AC,同理可得EH=
AC,同理可得EH=![]() BD,
BD,
则HG∥EF且HG=EF,
∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,
∴四边形EFGH为菱形.
矩形的中点四边形是菱形.理由如下:
连结AC、BD,如图所示:
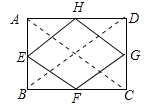
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH=![]() BD,FG=
BD,FG=![]() BD,EF=
BD,EF=![]() AC,GH=
AC,GH=![]() AC,
AC,
∵四边形ABCD是矩形,
∴AC=BD,∴EF=FG=GH=EH,
∴四边形EFGH是菱形.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形变换是( )
A.平移和旋转 B.对称和旋转 C.对称和平移 D.旋转和平移
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若xm=2,xn=4,则xm+n的值为 --------------------------------------------------- ( )
A. 6 B. 8 C. 16 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。
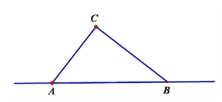
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
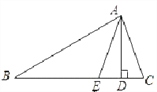
【题目】△ABC中,AD⊥BC,AE平分∠BAC交BC于点E.
(1)∠B=30°,∠C=70°,求∠EAD的大小;
(2)若∠B<∠C,则2∠EAD与∠C-∠B是否相等?若相等,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com