
分析 由已知等式知5xy=4x2+4y2-5,结合2xy≤x2+y2知5xy=4x2+4y2-5≤$\frac{5}{2}$(x2+y2),即可得x2+y2的最大值;由x2+y2≥-2xy知5xy=4x2+4y2-5≥-8xy-5,从而得xy≥$\frac{5}{13}$,即可由x2+y2≥-2xy≥$\frac{10}{13}$得出x2+y2的最小值.
解答 解:∵4x2-5xy+4y2=5,
∴5xy=4x2+4y2-5,
又∵2xy≤x2+y2,
∴5xy=4x2+4y2-5≤$\frac{5}{2}$(x2+y2),
设S=x2+y2,
4s-5≤$\frac{5}{2}$s,
∴s≤$\frac{10}{3}$即Smax=$\frac{10}{3}$,
∵x2+y2≥-2xy,
∴5xy=4x2+4y2-5≥-8xy-5,
∴xy≤-$\frac{5}{13}$,
∴-xy≥$\frac{5}{13}$,
∴S=x2+y2≥-2xy≥$\frac{10}{13}$,
∴Smin=$\frac{10}{13}$.
点评 本题主要考查配方法的应用,由已知等式结合2xy≤x2+y2、x2+y2≥-2xy得出x2+y2的范围是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
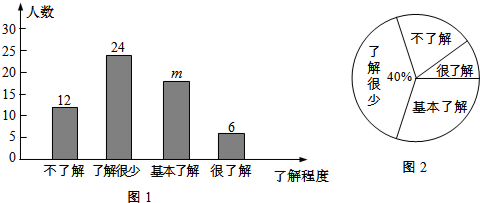
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com