

分析 (1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,在Rt△O′EM中,由sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,推出α=60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.列出方程即可解决问题、
(4)当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°.当N′落在AB上时,阴影部分面积最大,求出此时的面积即可.
解答 解:(1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE是矩形,EF=AM=1.想办法求出O′E的长即可.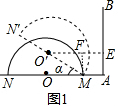
在Rt△MFO′中,∵∠MO$′\\;F$F=30°,MO′=2,
∴O′F=O′M•cos30°=$\sqrt{3}$,O′E=$\sqrt{3}$+1,
∴点O′到AB的距离为$\sqrt{3}$+1.
如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF是矩形,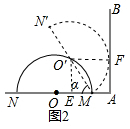
∴AE=O′F=2,
∵AM=1,
∴EM=1,
在Rt△O′EM中,sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,
∴α=60°
故答案为$\sqrt{3}$+1,60°.
(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.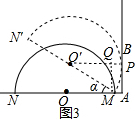
∵O′P=R,
∴R=$\frac{\sqrt{3}}{2}$R+1,
∴R=4+2$\sqrt{3}$.
(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.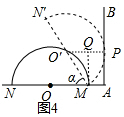
在Rt△O′QM中,O′Q=R•cosα,QP=m,
∵O′P=R,
∴R•cosα+m=R,
∴cosα=$\frac{R-m}{R}$.
故答案为$\frac{R-m}{R}$.
(4)如图5中,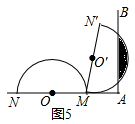
当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°
故答案为90°<α≤120°;
当N′落在AB上时,阴影部分面积最大,
所以S═$\frac{120•π•{m}^{2}}{360}$-$\frac{1}{2}$•$\sqrt{3}$m•$\frac{1}{2}$m=$\frac{π{m}^{2}}{3}$-$\frac{\sqrt{3}}{4}$m2.
点评 本题考查圆综合题、旋转变换、切线的判定和性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形或特殊四边形解决问题,所以中考压轴题.


科目:初中数学 来源: 题型:填空题
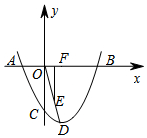 如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
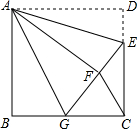 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,FC,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com