
分析 根据∠ABC=m°,分两种情况进行讨论:①当∠ABC=m°≤120°时,②当∠ABC=m°>120°时,分别根据角的和差关系进行计算,即可得出∠BCE的度数.
解答 解:分两种情况:
①如图所示,当0°<m°≤120°时,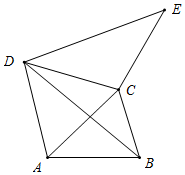
设∠BAC=α,∠ACB=β,则∠BAD=60°+α,α+β=180°-m°,
由旋转可得,∠ECD=∠BAD=60°+α,
∴∠BCE=360°-∠ACB-∠ACD-∠ECD
=360°-β-60°-(60°+α)
=240°-(α+β)
=240°-(180°-m°)
=60°+m°;
②如图所示,当120°<m°<180°时,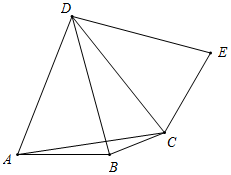
∠BAD=60°+α,α+β=180°-m°,
由旋转可得,∠ECD=∠BAD=60°+α,
∴∠BCE=∠ACB+∠ACD+∠ECD
=β+60°+60°+α
=120°+(α+β)
=120°+180°-m°
=300°-m°.
综上所述,∠BCE的度数为60°+m°或300°-m°.
故答案为:60°+m°或300°-m°.
点评 本题主要考查了旋转的性质以及等边三角形的性质,解决问题的关键是掌握:旋转前、后的图形全等,即对应角相等,对应边相等.解题时注意:等边三角形的三个角都是60°.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com