Question

图①是一个三角形，分别连接这个三角形三边的中点得到图②；再分别连接图②中间小三角形三边的中点，得到图③．

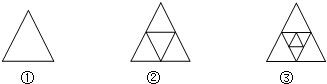
（1）图②有__________个三角形；图③有__________个三角形．

（2）按上面的方法继续下去，第5个图形中有__________个三角形；第n个图形中有__________个三角形？（用含有n的式子表示结论）

Answer 1

【考点】规律型：图形的变化类．

【专题】规律型．

【分析】（1）观察图形得到图①中三角形的个数为1，图②中三角形的个数为1+4，图③中三角形的个数为1+4×2；

（2）由（1）得到后面图形中的三角形个数比它前面它们的三角形个数多4，于是得到第n个图形中三角形的个数为1+4（n﹣1），则可计算出n=5时三角形的个数．

【解答】解：（1）图①中三角形的个数为1，

图②中三角形的个数为1+4=5，

图③中三角形的个数为1+4×2=9；

（2）图⑤中三角形的个数为1+4×4=17；

第n个图形中三角形的个数为1+4（n﹣1）．

故答案为5，9；17；1+4（n﹣1）．

【点评】本题考查了规律型﹣图形的变化类：首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．