
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

【答案】D(2,0)
【解析】(1)找到AB,BC的垂直平分线的交点即为圆心坐标;
(2)利用勾股定理可求得圆的半径;易得△AOD≌△DEC,那么∠OAD=∠CDE,即可得到圆心角的度数为90°;
(3)求得弧长,除以2π即为圆锥的底面半径.
解:(1)如图;D(2,0)

(2)如图;AD=![]() =
=![]() =2
=2![]() ;
;
作CE⊥x轴,垂足为E.
∵△AOD≌△DEC,
∴∠OAD=∠CDE,
又∵∠OAD+∠ADO=90°,
∴∠CDE+∠ADO=90°,
∴扇形DAC的圆心角为90度;
(3)∵弧AC的长度即为圆锥底面圆的周长.l弧=![]() =
=![]() =
=![]() π,
π,
设圆锥底面圆半径为r,则2πr=![]() π,
π,
∴r=![]() .
.
“点睛”本题用到的知识点为:非直径的弦的垂直平分线经过圆心;圆锥的弧长等于底面周长.


科目:初中数学 来源: 题型:
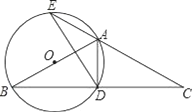
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
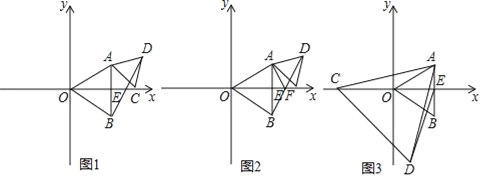
【题目】如图△AOB和△ACD是等边三角形,其中AB⊥x轴于E点.
(1)如图,若OC=5,求BD的长度;
(2)设BD交x轴于点F,求证:∠OFA=∠DFA;
(3)如图,若正△AOB的边长为4,点C为x轴上一动点,以AC为边在直线AC下方作正△ACD,连接ED,求ED的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com