
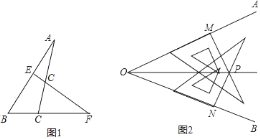
【题目】(1)如图1在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=45°,
∠F=30°,∠CGF=70°,求∠A的度数.
(2)利用三角板也能画出一个角的平分线,画法如下:①利用三角板在∠AOB的两边上分
别取OM=ON:②分别过点M、N画OM、ON的垂线,交点为![]() ;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
【答案】(1)35°;(2)详见解析.
【解析】
(1)利用对顶角线段得到∠AGE=70°,再根据三角形外角性质得∠AEF=∠B+∠F=75°,然后根据三角形内角和计算∠A的度数;
(2)由作图得∠PMO=∠PNO=90°,则可根据“HL”可证明Rt△PMO≌Rt△PNO,所以∠POM=∠PON,从而可判断射线OP为∠AOB的角平分线.
(1)∵∠CGF=70°,
∴∠AGE=70°,
∵∠B=45°,∠F=30°,
∴∠AEF=∠B+∠F=75°,
∴∠A=180°﹣75°﹣70°=35°;
(2)证明:这种作法的正确.
理由如下:由作图得∠PMO=∠PNO=90°,
在Rt△PMO和Rt△PNO中
![]() ,
,
∴Rt△PMO≌Rt△PNO,
∴∠POM=∠PON,
即射线OP为∠AOB的角平分线.


科目:初中数学 来源: 题型:
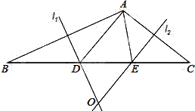
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆, ![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.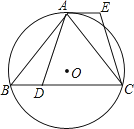
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表为甲班55人某次数学小考成绩的统计结果,关于甲班男、女生此次小考成绩的统计量,下列叙述何者正确?( )
成绩(分) | 50 | 70 | 90 |
男生(人) | 10 | 10 | 10 |
女生(人) | 5 | 15 | 5 |
合计(人) | 15 | 25 | 15 |
A.男生成绩的四分位距大于女生成绩的四分位距
B.男生成绩的四分位距小于女生成绩的四分位距
C.男生成绩的平均数大于女生成绩的平均数
D.男生成绩的平均数小于女生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:4,则k值为何?( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
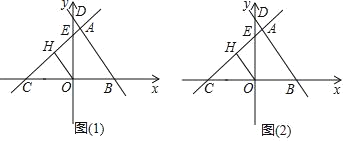
【题目】如图(1),平面直角坐标系中,直线y=![]() 与x轴、y轴分别交于点B、D,直线y=
与x轴、y轴分别交于点B、D,直线y=![]() 与x轴、y轴分别交于点C、E,且两条直线交于点A.
与x轴、y轴分别交于点C、E,且两条直线交于点A.
(1)若OH⊥CE于点H,求OH的长.
(2)求四边形ABOE的面积.
(3)如图(2),已知点F(﹣![]() ,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(
,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C顺时针旋转60°得△ADC,连接OD.当AO=5,BO=4,α=150°时,则CO的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在云南省某市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 
你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;扇形统计图中甲类部分的圆心是 .
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2400人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com