
【题目】如图,直线y=kx+b过x轴上的点A(2,0),且与抛物线![]() 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1).
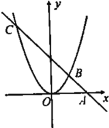
(1)求直线与抛物线对应的函数表达式;
(2)当![]() 时,请根据图象写出自变量x的取值范围;
时,请根据图象写出自变量x的取值范围;
(3)抛物线上是否存在一点D,使![]() ?若存在,求出D点坐标;若不存在,请说明理由
?若存在,求出D点坐标;若不存在,请说明理由
【答案】(1)y=x+2,y=x2(2)-2<x<1(3) (![]() ,3)或(
,3)或(![]() ,3)
,3)
【解析】
(1)已知直线AB经过A(2,0),B(1,1),设直线表达式为y=ax+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
(2)求出B,C的坐标,根据图像即可求解;
(3)已知A,B,C三点坐标,根据作差法可求△OBC的面积,在△DOA中,已知面积和底OA,可求OA上的高,即D点纵坐标,代入抛物线解析式求横坐标,得出D点坐标.
(1)设直线AB关系式为y=kx+b
∵A(2,0),B(1,1)都在直线y=kx+b的图象上,
∴![]() 解得
解得![]() ,
,
∴直线AB关系式为y=x+2,
∵点B(1,1)在y=ax2的图象上,
∴a=1,其关系式为y=x2;
(2)由题意得![]() ,
,
解得![]() 或
或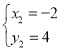
∴C(-2,4)
由图像可知![]() 表示一次函数在二次函数上方,
表示一次函数在二次函数上方,
故x的取值为-2<x<1;
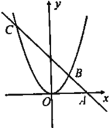
(3)如图,存在点D,设D(x,x2),
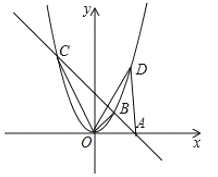
∴S△OAD=![]() |OA||yD|=
|OA||yD|=![]() ×2×x2=x2
×2×x2=x2
∵C(2,4),
∴S△BOC=S△AOCS△OAB=![]() ×2×4
×2×4![]() ×2×1=3,
×2×1=3,
∵S△BOC=S△OAD,
∴x2=3,
解得x=±![]() ,
,
∴点D坐标为(![]() ,3)或(
,3)或(![]() ,3).
,3).


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
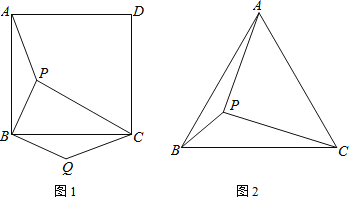
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
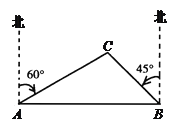
【题目】已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.
(1)请直接写出点(2,2)的“关联点”的坐标;
(2)如果点P在函数y=x﹣1的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
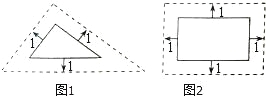
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
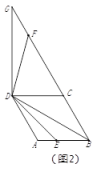
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
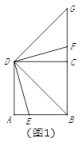
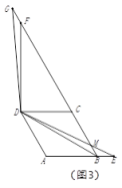
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
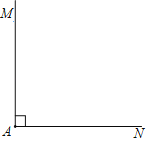
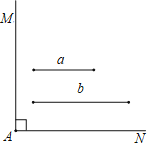
【题目】已知:如图,∠MAN=90°,线段a和线段b
求作:矩形ABCD,使得矩形ABCD的两条边长分别等于线段a和线段b.
下面是小东设计的尺规作图过程.
作法:如图,
①以点A为圆心,b为半径作弧,交AN于点B;
②以点A为圆心,a为半径作弧,交AM于点D;
③分别以点B、点D为圆心,a、b长为半径作弧,两弧交于∠MAN内部的点C;
④分别连接BC,DC.
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:
∵AB= ;AD= ;
∴四边形ABCD是平行四边形.
∵∠MAN=90°;
∴四边形ABCD是矩形( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com