
����Ŀ���ƻ�С˵��ʵ���ҵĹ��¡��У�������һ����ڣ���ѧ�Ұ�һ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ���¼������ֲ��߶ȵ�������������±�����
�¶�x/�� | �� | ��4 | ��2 | 0 | 2 | 4 | 6 | �� |
ֲ��ÿ��߶ȵ�������y/mm | �� | 41 | 49 | 49 | 41 | 25 | 1 | �� |
����Щ���ݣ���ѧ���Ʋ��ֲ��ÿ��߶ȵ�������y���¶�x�Ķ��κ�������ô�����������ۣ�
�ٸ�ֲ����0��ʱ��ÿ��߶ȵ����������
�ڸ�ֲ���ک�6��ʱ��ÿ��߶ȵ��������ܱ�����25mm���ң�
�۸�ֲ��������ֲ�ﲻͬ��6�����ϵĻ����¸߶ȼ���������.
���������У�������ȷ���۵������
A. �٢ڢ� B. �٢� C. �٢� D. �ڢ�
���𰸡�D
��������
��1����Ϊ�Ƕ��κ�����������y=ax2+bx+c��a��0����Ȼ��ѡ��x=-2��0��2�������ݣ����ô���ϵ��������κ�������ʽ���Ѷ��κ�������ʽ�����ɶ���ʽ��ʽ���ٸ��ݶ��κ�������ֵ������
(1)��Ϊ�Ƕ��κ���,������y=ax2+bx+c(a��0)��
��x=2ʱ��y=49��
x=0ʱ��y=49��
x=2ʱ��y=41��
�ֱ�������ʽ��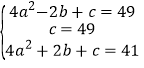 �����
�����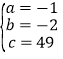 ,
,
��,y����x�ĺ�����ϵʽΪ��
��y=x22x+49=(x+1)2+50��
A=-1<0,�����߿������ϣ�
����x=1ʱ��y�����ֵΪ50��
�����¶�Ϊ1��ʱ����������ÿ��߶����������
�ʢٴ���.
��2����x= -6�������ʽy=x22x+49�ã�y=25��
�ʢ���ȷ.
��3����x= 6�������ʽy=x22x+49�ã�y=1
��x= 7�������ʽy=x22x+49�ã�y= -14<0,
�ʢ���ȷ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����⣺
�����θ��ͣ�
��������ͼ1��![]() ��ֱ��
��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮
���⣺��ֱ��![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ
��ʹ![]() ��ֵ��С��
��ֵ��С��
����������![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ,
,
��������֮�䣬�߶��������֪����![]() ��Ϊ����ĵ㣮
��Ϊ����ĵ㣮
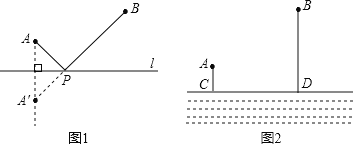
��ģ��Ӧ�ã�
��ͼ2��ʾ������![]() ��һ����
��һ����![]() ��ͬ�࣬
��ͬ�࣬![]() ���嵽�ӱ�
���嵽�ӱ�![]() �ľ���ֱ���
�ľ���ֱ���![]() ǧ��,
ǧ��,![]() ǧ��,
ǧ��, ![]() ǧ�ף���Ҫ�ںӱ�
ǧ�ף���Ҫ�ںӱ�![]() �Ͻ���һˮ������
�Ͻ���һˮ������![]() ������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������
������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������![]() ��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���
��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���![]() ��
��
����չ���죩
��ͼ��![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() �������
��С�����![]() Ӧ�����㣨 ����Ψһѡ����ȷ��
Ӧ�����㣨 ����Ψһѡ����ȷ��
A�� ![]() B��
B�� ![]()
C�� ![]() D��
D�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
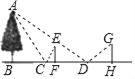
����Ŀ��ijһ�죬С����С������һ�ӱߣ�����ƽ�澵��Ƥ�߲��������ӵĴ��¿��ȣ�������ȷ���ް�ȫ����������£����ںӰ���ѡ����һ��C����C��Ӷ������ϵ�һ�����ĵײ���B��ȷ����ֱ�ߴ�ֱ�ںӰ�����С����F��ʱ������ƽ�澵�п�������A��С���ڵ�D����ƽ�澵��С����H��ʱ������ƽ�澵�п�������A����F��D��H����BC���ӳ����ϣ�С�����۾������ĸ߶�EF=1.5m��С�����۾������ĸ߶�GH=1.6m�����CF=1m��DH=2m��CD=8.4m��AB��BH��EF��BH��GH��BH���������ϲ������̼��������ݣ���������ӿ�BC�Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��5����B����1��0����C����4��3����
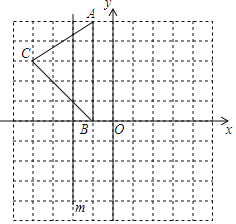
��1����ͼ��������ABC����m��ֱ��m�ϵĺ����궼Ϊ��2���ĶԳ�ͼ����A1B1C1��
��2���߶�����һ��P����![]() ��
��![]() ����ֱ��д����P����ֱ��m�ԳƵĵ�������� ����
����ֱ��д����P����ֱ��m�ԳƵĵ�������� ����
��3���߶�BC����һ��M��a��b������M����ֱ��m�ĶԳƵ�N��c��d������ֱ��д��a��c�Ĺ�ϵ���� ����b��d�Ĺ�ϵ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
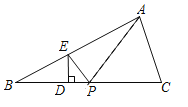
����Ŀ���Ķ�����ͼ1������ABC�У�BE��AC���ϵ����ߣ� D��BC������һ����CD��BD=1��2��AD��BE�ཻ�ڵ�P����![]() ��ֵ��С껷��֣�����A��AF��BC����BE���ӳ����ڵ�F��ͨ��������AEF�����������ͼ����ܹ�ʹ����õ��������ͼ2����
��ֵ��С껷��֣�����A��AF��BC����BE���ӳ����ڵ�F��ͨ��������AEF�����������ͼ����ܹ�ʹ����õ��������ͼ2����


��1��![]() ��ֵΪ ��
��ֵΪ ��
��2���ο�С�˼������ķ�����������⣺
��ͼ3������ABC�У���ACB=90�㣬��D��BC���ӳ����ϣ�AD��AC���ϵ�����BE���ӳ��߽��ڵ�P��DC��BC��AC=1��2��3 ��
![]() ��
��![]() ��ֵ��
��ֵ��
![]() ��CD=2����BP�ij���
��CD=2����BP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ��ԳƵ�ʱ����ʦ��ͬѧ��˼���α��е�̽���⣮
��ͼ��1����Ҫ��ȼ���ܵ�l����һ����վ���ֱ���A��B����������վ���ڹܵ���ʲô�ط�����ʹ���õ�����������̣�
�������l���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ��������![]() ���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ�
���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ�
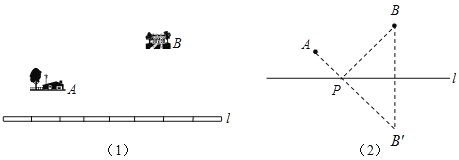
������С��ͨ������˼�����ܿ�ó��˽������������ȷ�취�����ѹܵ�l����һ��ֱ�ߣ�ͼ��2�����������ת��Ϊ��Ҫ��ֱ��l����һ��P��ʹAP��BP�ĺ���С�����������������ģ�
������B����ֱ��l�ĶԳƵ�B����
������AB����ֱ��l�ڵ�P�����PΪ����
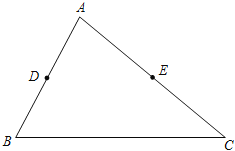
����ο�С������������������⣮��ͼ����ABC�У���D��E�ֱ���AB��AC�ߵ��е㣬BC=6��BC���ϵĸ�Ϊ4��������BC����ȷ��һ��P��ʹ��PDE���ܳ���С��
��1����ͼ��������P��������ͼ�ۼ�����д��������
��2����ֱ��д����PDE�ܳ�����Сֵ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵxOy�У��������P�Ƶ�T��0��t����t��0����ת180��õ���Q����ô���߶�QPΪ����չ��������QΪ��P�ġ���չ�㡱��
��1����t=3ʱ������0��0���ġ���չ��������Ϊ ��������1��1��������չ�㡱����Ϊ ��
��2����� t��1������M��2��1���ġ���չ�㡱N�ں���y=��![]() ��ͼ����ʱ����t��ֵ��
��ͼ����ʱ����t��ֵ��
��3����t=1ʱ����QΪ��P��2��0���ġ���չ�㡱����������� y=��x��m��2��1�롰��չ����PQ�н��㣬��m��ȡֵ��Χ��
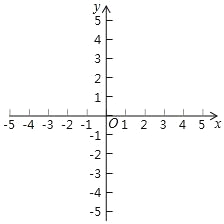
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
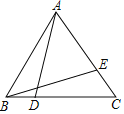
����Ŀ����ͼ���ȱ�������ABC�У�![]() ����D��ֱ��BC�ϣ���E��ֱ��AC�ϣ���
����D��ֱ��BC�ϣ���E��ֱ��AC�ϣ���![]() ����
����![]() ʱ����AE�ij�Ϊ______��
ʱ����AE�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
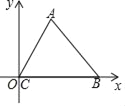
����Ŀ����ͼ����ֱ������ϵ�У��߳�Ϊ1������ABC��C��O�غϣ��ı�BC��x���ϣ�����A�ڵ�һ���ޣ����ڽ������²�����
��1������ABC��x������ƽ��һ����λ���ȣ���ʱA��ΪA1��
��2������������x�ᷭ�ۣ���ʱA1��ΪA2��
��3�����������Ƶ�O��ת180�㣬��ʱA2��ΪA3��
��4������������y�ᷭ�ۣ���ʱA3��ΪA4��
��5�����������Ƶ�O��ת180�㣬��ʱA4��ΪA5��
���մ˹��ɣ��ظ������岽����A2018������Ϊ��������
A. ��![]() ����
����![]() �� B. ����
�� B. ����![]() ��
��![]() �� C. ��
�� C. ��![]() ��
��![]() �� D. ����
�� D. ����![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com