
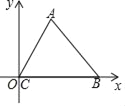
����Ŀ����ͼ����ֱ������ϵ�У��߳�Ϊ1������ABC��C��O�غϣ��ı�BC��x���ϣ�����A�ڵ�һ���ޣ����ڽ������²�����
��1������ABC��x������ƽ��һ����λ���ȣ���ʱA��ΪA1��
��2������������x�ᷭ�ۣ���ʱA1��ΪA2��
��3�����������Ƶ�O��ת180�㣬��ʱA2��ΪA3��
��4������������y�ᷭ�ۣ���ʱA3��ΪA4��
��5�����������Ƶ�O��ת180�㣬��ʱA4��ΪA5��
���մ˹��ɣ��ظ������岽����A2018������Ϊ��������
A. ��![]() ����
����![]() �� B. ����
�� B. ����![]() ��
��![]() �� C. ��
�� C. ��![]() ��
��![]() �� D. ����
�� D. ����![]() ����
����![]() ��
��
 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƻ�С˵��ʵ���ҵĹ��¡��У�������һ����ڣ���ѧ�Ұ�һ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ���¼������ֲ��߶ȵ�������������±�����
�¶�x/�� | �� | ��4 | ��2 | 0 | 2 | 4 | 6 | �� |
ֲ��ÿ��߶ȵ�������y/mm | �� | 41 | 49 | 49 | 41 | 25 | 1 | �� |
����Щ���ݣ���ѧ���Ʋ��ֲ��ÿ��߶ȵ�������y���¶�x�Ķ��κ�������ô�����������ۣ�
�ٸ�ֲ����0��ʱ��ÿ��߶ȵ����������
�ڸ�ֲ���ک�6��ʱ��ÿ��߶ȵ��������ܱ�����25mm���ң�
�۸�ֲ��������ֲ�ﲻͬ��6�����ϵĻ����¸߶ȼ���������.
���������У�������ȷ���۵������
A. �٢ڢ� B. �٢� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ֽ���ʽ![]() ������ֱ��д�����������
������ֱ��д�����������![]() ����������
����������![]() һ���ܱ�һ������������������������ֵ��������
һ���ܱ�һ������������������������ֵ��������
��2���Ķ�����������⣺
�ֽ���ʽ![]()
�⣺��![]() ����ԭʽ
����ԭʽ![]()
�����Ľ��ⷽ����������Ԫ�������������ӵĶ���ʽ�У�ijһ�����ظ�����ʱ����������ĸ�����滻���Ӷ����������ʽ����Ԫ����һ����Ҫ����ѧ�����������������û�Ԫ������������á���Ԫ���������ж���ʽ������ʽ�ֽ⣺
��![]()
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��2k+1��x+k2+1=0����������ʵ��![]() ��
��
��1����ʵ��k��ȡֵ��Χ��
��2����������ʵ��![]() �����x1��+��x2��=x1��x2����k��ֵ��
�����x1��+��x2��=x1��x2����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
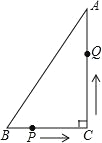
����Ŀ����ͼ����Rt��ABC�У�AC��8cm��BC��6cm��P����BC�ϣ���B�㵽C���˶��������� C�������� P�˶����ٶ�Ϊ1cm/s��Q����AC�ϴ�C���˶���A����������A�������ٶ�Ϊ2cm/s������ P��Q �ֱ��B��C ͬʱ�˶������˶�ʱ���Ϊt�룬������������⣬��д��̽������Ҫ���̣�
��1���� t Ϊ��ֵʱ��P��Q ����ľ���Ϊ 4![]() cm��
cm��
��2�������䷽��˵������P�˶�����ʱ��ʱ���ı���BPQA�������С����С����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
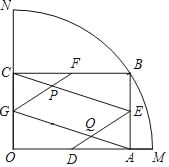
����Ŀ����ͼ������OMN�İ뾶Ϊ1��Բ�Ľ�Ϊ90�㣬��B��![]() ��һ���㣬BA��OM�ڵ�A��BC��ON�ڵ�C����D��E��F��G�ֱ����߶�OA��AB��BC��CO���е㣬GF��CE�ཻ�ڵ�P��DE��AG�ཻ�ڵ�Q��
��һ���㣬BA��OM�ڵ�A��BC��ON�ڵ�C����D��E��F��G�ֱ����߶�OA��AB��BC��CO���е㣬GF��CE�ཻ�ڵ�P��DE��AG�ཻ�ڵ�Q��
��1������B�ƶ���ʹAB��OA=![]() ��3ʱ����
��3ʱ����![]() �ij���
�ij���
��2������B�ƶ���ʹ�ı���EPGQΪ����ʱ����AM�ij���
��3������PQ����˵��3PQ2+OA2�Ƕ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
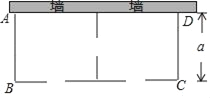
����Ŀ��ijũ��Ҫ��һ����������������ABCD������������һ�濿ǽ��ǽ�����ó���Ϊ27�ף�����������ľ��Χ�ɣ��м�Ҳ��ľ���������ֳ��������أ�������ͼ��ʾ����������1�����ţ�����ľ���������ɺ�ľ���ܳ�57�ף�����������������ABCD���Ŀ�Ϊa�ף�
��1���������ij�Ϊ�����ף��ú�a�Ĵ���ʽ��ʾ����
��2���������������Ϊ288m2����a��ֵ��
��3����aΪ��ֵʱ����������������ʱ�������ﵽ��������Ϊ����ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ������ó߹���ͼ����������⣺
��֪����OAB.
��������O��ʹ��O����OAB�ı�AB����.

С�����������£�
��ͼ����ȡ�߶�OB���е�M����MΪԲ�ģ�MOΪ�뾶����M�����AB���ڵ�C��
����OΪԲ�ģ�OCΪ�뾶����O��
���ԣ���O������������Բ.

��ش���������������__________________________________________________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com