
����Ŀ���Ķ�����⣺
�����θ��ͣ�
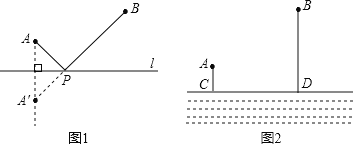
��������ͼ1��![]() ��ֱ��
��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮
���⣺��ֱ��![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ
��ʹ![]() ��ֵ��С��
��ֵ��С��
����������![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ,
,
��������֮�䣬�߶��������֪����![]() ��Ϊ����ĵ㣮
��Ϊ����ĵ㣮
��ģ��Ӧ�ã�
��ͼ2��ʾ������![]() ��һ����
��һ����![]() ��ͬ�࣬
��ͬ�࣬![]() ���嵽�ӱ�
���嵽�ӱ�![]() �ľ���ֱ���
�ľ���ֱ���![]() ǧ��,
ǧ��,![]() ǧ��,
ǧ��, ![]() ǧ�ף���Ҫ�ںӱ�
ǧ�ף���Ҫ�ںӱ�![]() �Ͻ���һˮ������
�Ͻ���һˮ������![]() ������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������
������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������![]() ��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���
��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���![]() ��
��
����չ���죩
��ͼ��![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() �������
��С�����![]() Ӧ�����㣨 ����Ψһѡ����ȷ��
Ӧ�����㣨 ����Ψһѡ����ȷ��
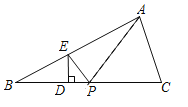
A�� ![]() B��
B�� ![]()
C�� ![]() D��
D�� ![]()
���𰸡���ģ��Ӧ�á�ͼ����������ʡ������ܵ�������10000Ԫ������չ���졿D
��������
1.��ģ��Ӧ�á���������ˮ�ܵĹ��̷���Ϊÿǧ��15000Ԫ����һ����ֵ������Ҫ��CD��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ����˼����CD����һ��P��ʹAP��BP�ĺ���С����![]() ��A�ĶԳƵ㣬ʹAP+BP��̾���ʹ
��A�ĶԳƵ㣬ʹAP+BP��̾���ʹ![]() ��̣�
��̣�
2.����չ���졿����E����ֱ��BC�ĶԳƵ�F������AF��BC��P����ʱPA+PE��ֵ��С��������ԳƵ����ʼ��ɵõ���APC=��DPE��
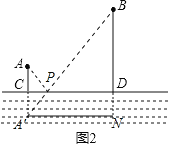
1.��ģ��Ӧ�á�
��ͼ��ʾ���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ,
,
��![]() ������ѡ���λ�ã�
������ѡ���λ�ã�
��![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ��
��
��![]() ��
��
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]() ��
��![]() ��
��
��ֱ��������![]() ��,
��, ![]() ,
,
![]() ǧ�ף�
ǧ�ף�
�����·��![]() ǧ�ף�
ǧ�ף�
��ʡ������ܵ�������![]() (Ԫ)��
(Ԫ)��
2.����չ���졿
��ͼ������E����ֱ��BC�ĶԳƵ�F������AF��BC��P����ʱPA+PE��ֵ��С��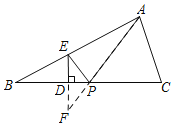
�ɶԳ��Կ�֪����DPE=��FPD��
�ߡ�APC=��FPD��
���APC=��DPE��
��PA+PE��Сʱ����PӦ�������APC=��DPE��
��ѡ��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
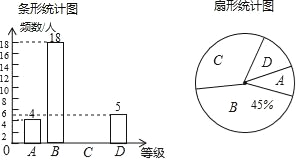
����Ŀ���������������п������ؿ���Ŀ֮һ��������ijѧУΪ�˽������꼶ѧ�������������������������ȡ���־��꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ������²�������ͳ��ͼ����˵����A����8�֩�10�֣�B����7�֩�7.9�֣�C����6�֩�6.9�֣�D����1�֩�5.9�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ�����ε�Բ�Ľ����� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ���������� ���ȼ���
��4����У���꼶��300��ѧ�������������������Գɼ��ﵽA����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС����̽�������ڽǶ���ȵ�Բ�ڽӶ�����Ƿ�Ϊ������Ρ�ʱ��������̽�֣�
��ͬѧ���ҷ������ֶ���β�һ����������Σ���Բ�ڽӾ��β�һ���������Σ�
��ͬѧ����֪������Ϊ3ʱ�������������Σ����룬����Ϊ5ʱ��������Ҳ��������Ρ�
��ͬѧ���ҷ��ֱ���Ϊ6ʱ����Ҳ��һ�����������Σ���ͼ2����ABC���������Σ���AD����BE����CF����ȣ����������������ADBECF�����������Σ�
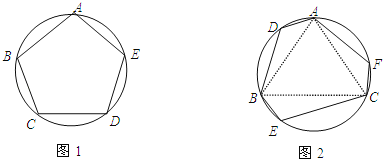
��1����ͼ1����Բ�ڽ������ABCDE�ĸ��ڽǾ���ȣ�����ABC= �㣬����Ҫ˵��Բ�ڽ������ABCDEΪ������ε����ɣ�
��2����ͼ2����֤����ͬѧ����������θ��ڽ���ȣ�
��3����������̽�����̣������⡰���ڽǶ���ȵ�Բ�ڽӶ�����Ƿ�Ϊ������Ρ��Ľ����롰����n��n��3��nΪ���������Ĺ�ϵ�������IJ��루����֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
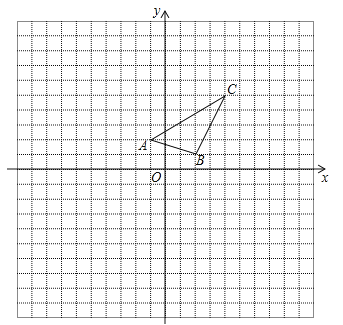
����Ŀ����ͼ���ڱ߳�Ϊ1�������������н���ƽ��ֱ������ϵ����֪��ABC��������ֱ�ΪA����1��2����B��2��1����C��4��5����
��1��������ABC����x�ԳƵ���A1B1C1��
��2����ԭ��OΪλ�����ģ���x����Ϸ�������A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2���������A2B2C2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
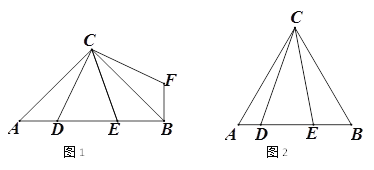
����Ŀ����ͼ����ABC��AC=BC����D��E��AB���ϣ�����CD��CE��
(1)��ͼ1�������ACB=90�������߶�CD��ʱ����ת90�����õ��߶�CF������BF��
����֤����ACD�ա�BCF��
������DCE=45���� ��֤��DE2=AD2+BE2��
(2)��ͼ2�������ACB=60������DCE=30�����õ�ʽ��ʾAD��DE��BE�����߶ε�������ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����������õĿ�չ����������һ������������˽⣺����ĵ��۱�����ĵ��۶�20Ԫ����1000Ԫ��������ĸ�������800Ԫ��������ĸ�����ͬ��
��1����������ĵ��۸��Ƕ���Ԫ��
��2����ѧУ���㹺������������������100�����ҹ�����ܷ��ò�����9600Ԫ��������ܹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
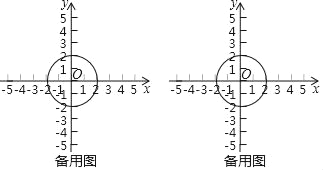
����Ŀ����P����dֵ���������£�����QΪԲ������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P����dֵ������ΪdP���ر�ģ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0������O�İ뾶Ϊ2ʱ��
��1������C����![]() ��0����D��3��4������dc=�� ����dp=�� ����
��0����D��3��4������dc=�� ����dp=�� ����
��2������ֱ��y=2x+2�ϴ��ڵ�P��ʹ��dP=2�������P�ĺ����ꣻ
��3��ֱ��y=��![]() x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
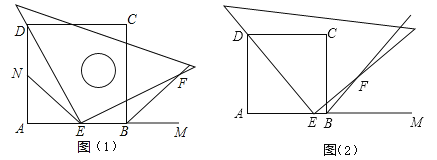
����Ŀ����ͼ��ʾ���ı���![]() �������Σ�
�������� ![]() ��
��![]() �ӳ�����һ�㣮ֱ�����dzߵ�һ��ֱ�DZ߾�����
�ӳ�����һ�㣮ֱ�����dzߵ�һ��ֱ�DZ߾�����![]() ����ֱ�Ƕ���
����ֱ�Ƕ���![]() ��
��![]() ���ϻ���(��
���ϻ���(��![]() �����
�����![]() �غ�)����һֱ�DZ���
�غ�)����һֱ�DZ���![]() ��ƽ����
��ƽ����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
(1)��֤: ![]() ;
;
(2)��ͼ(1)������![]() ��
��![]() �ߵ��е�λ��ʱ������
�ߵ��е�λ��ʱ������![]() ��
��![]() ��������ϵ����֤����IJ���;
��������ϵ����֤����IJ���;
(3)��ͼ(2)������![]() ��
��![]() ��(�����˵�)�ϵ�����λ��ʱ�������ʱ
��(�����˵�)�ϵ�����λ��ʱ�������ʱ![]() ��
��![]() ��������������ϵ����֤����IJ��룮
��������������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƻ�С˵��ʵ���ҵĹ��¡��У�������һ����ڣ���ѧ�Ұ�һ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ���¼������ֲ��߶ȵ�������������±�����
�¶�x/�� | �� | ��4 | ��2 | 0 | 2 | 4 | 6 | �� |
ֲ��ÿ��߶ȵ�������y/mm | �� | 41 | 49 | 49 | 41 | 25 | 1 | �� |
����Щ���ݣ���ѧ���Ʋ��ֲ��ÿ��߶ȵ�������y���¶�x�Ķ��κ�������ô�����������ۣ�
�ٸ�ֲ����0��ʱ��ÿ��߶ȵ����������
�ڸ�ֲ���ک�6��ʱ��ÿ��߶ȵ��������ܱ�����25mm���ң�
�۸�ֲ��������ֲ�ﲻͬ��6�����ϵĻ����¸߶ȼ���������.
���������У�������ȷ���۵������
A. �٢ڢ� B. �٢� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com