
【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
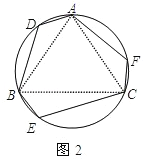
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
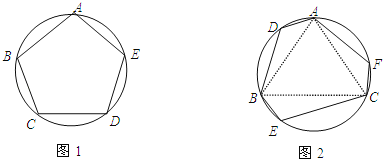
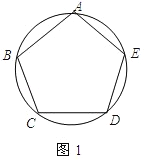
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC= °,并简要说明圆内接五边形ABCDE为正五边形的理由;
(2)如图2,请证明丙同学构造的六边形各内角相等;
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
【答案】(1)108.见解析;(2)见解析;(3)见解析
【解析】
试题分析:(1)运用n边形的内角和定理就可求出∠ABC的度数;已知圆内接五边形ABCDE的各内角均相等,要证该五边形为正五边形,只需证该五边形的各边均相等,只需利用弧与圆周角之间的等量关系就可解决问题.
(2)由△ABC是正三角形可得∠ABC=∠ACB=∠BAC=60°,根据圆内接四边形的性质可得∠AFC、∠ADB、∠BEC均为120°,由![]() =
=![]() 可得∠ABD=∠CAF,即可求出∠DAF=120°,同理可得∠DBE=∠ECF=120°,问题得以解决.
可得∠ABD=∠CAF,即可求出∠DAF=120°,同理可得∠DBE=∠ECF=120°,问题得以解决.
(3)依据对(1)、(2)的探索积累的经验就可提出合理的猜想.
解:(1)∵五边形的内角和=(5﹣2)×180°=540°,
∴∠ABC=![]() =108°.
=108°.
故答案为:108.
理由:如图1,
∵∠A=∠B
∴![]() =
=![]() ,
,
∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() ,
,
∴![]() =
=![]() ,
,
∴BC=AE.
同理可得:BC=DE,DE=AB,AB=CD,CD=AE,
∴BC=DE=AB=CD=AE,
∴五边形ABCDE是正五边形;
(2)证明:如图2,
∵△ABC是正三角形,
∴∠ABC=∠ACB=∠BAC=60°,
∵四边形ABCF是圆内接四边形,
∴∠ABC+∠AFC=180°,
∴∠AFC=120°.
同理可得:∠ADB=120°,∠BEC=120°.
∵∠ADB=120°,
∴∠DAB+∠ABD=60°.
∵![]() =
=![]() ,
,
∴∠ABD=∠CAF,
∴∠DAB+∠CAF=60°,
∴∠DAF=∠DAB+∠CAF+∠BAC=120°.
同理可得:∠DBE=120°,∠ECF=120°,
∴∠AFC=∠ADB=∠BEC=∠DAF=∠DBE=∠ECF=120°,
故图2中六边形各角相等;
(3)由(1)、(2)可提出以下猜想:
当n(n≥3,n为整数)是奇数时,各内角都相等的圆内接多边形是正多边形;
当n(n≥3,n为整数)时偶数时,各内角都相等的圆内接多边形不一定为正多边形.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨(x>14),应交水费为y元,请写出y与x之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),
D(-2,-2),E(0,-3)。

(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(-2,-2),E(0,-3),判断直线l与⊙P的位置关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
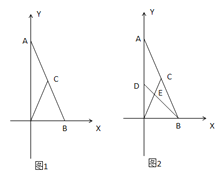
【题目】如图1,在平面直角坐标系中,已知点![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)如图2,![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试探索
,试探索![]() 是否为定值?若是,求出该值;若不是,请说明理由;
是否为定值?若是,求出该值;若不是,请说明理由;
(3)点![]() 为坐标轴上一点,请直接写出满足
为坐标轴上一点,请直接写出满足![]() 为等腰三角形的所有点
为等腰三角形的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
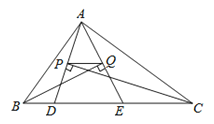
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解答题:
(几何概型)
条件:如图1:![]() 是直线
是直线![]() 同旁的两个定点.
同旁的两个定点.
问题:在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的值最小;
的值最小;
方法:作点![]() 关于直线
关于直线![]() 对称点
对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
由“两点之间,线段最短”可知,点![]() 即为所求的点.
即为所求的点.
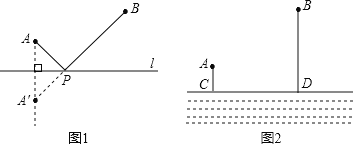
(模型应用)
如图2所示:两村![]() 在一条河
在一条河![]() 的同侧,
的同侧,![]() 两村到河边
两村到河边![]() 的距离分别是
的距离分别是![]() 千米,
千米,![]() 千米,
千米, ![]() 千米,现要在河边
千米,现要在河边![]() 上建造一水厂,向
上建造一水厂,向![]() 两村送水,铺设水管的工程费用为每千米20000元,请你在
两村送水,铺设水管的工程费用为每千米20000元,请你在![]() 上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用
上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用![]() .
.
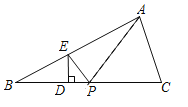
(拓展延伸)
如图,![]() 中,点
中,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一个动点,连接
上一个动点,连接![]() ,若
,若![]() 最小,则点
最小,则点![]() 应该满足( )(唯一选项正确)
应该满足( )(唯一选项正确)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
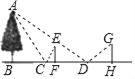
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com