
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?

【答案】(1)见解析;(2)当t=5时,DP⊥AC,理由见解析
【解析】
(1)根据矩形的性质可得CD∥AB,根据平行线的性质可得∠DCQ=∠QAP,∠PDC=∠QPA,进而可得判定△APQ∽△CDQ;
(2)首先证明△ADQ∽△ACD,根据相似三角形的性质可得![]() ,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得
,然后计算出AC长,进而可得AQ长,再证明△AQP∽△ABC,可得![]() ,则
,则![]() ,再解即可得到t的值.
,再解即可得到t的值.
(1)证明:∵四边形ABCD是矩形,
∴CD∥AB,
∴∠DCQ=∠QAP,∠PDC=∠QPA,
∴△APQ∽△CDQ;
(2)解:当t=5时,DP⊥AC;
∵∠ADC=90°,DP⊥AC,
∴∠AQD=∠AQP=∠ADC=90°,
∵∠DAQ=∠CAD,
∴△ADQ∽△ACD,
∴![]() ,
,
AC=![]() ,
,
则AQ=![]() ,
,
∵∠AQP=∠ABC=90°,∠QAP=∠BAC,
∴△AQP∽△ABC,
∴![]() ,
,
则![]() ,
,
解得:t=5,
即当t=5时,DP⊥AC.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
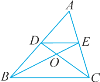
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,连接BE,CD相交于点O,连接DE,下列结论:①![]() =
=![]() ;②
;②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[m﹣1,1+m,﹣2m]的函数的一些结论:①当m=3时,函数图象的顶点坐标是(﹣1,﹣8);②当m>1时,函数图象截x轴所得的线段长度大于3;③当m<0时,函数在x>![]() 时,y随x的增大而减小;④不论m取何值,函数图象经过两个定点.其中正确的结论有( )
时,y随x的增大而减小;④不论m取何值,函数图象经过两个定点.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
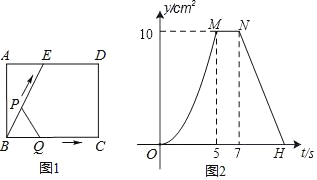
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
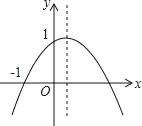
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
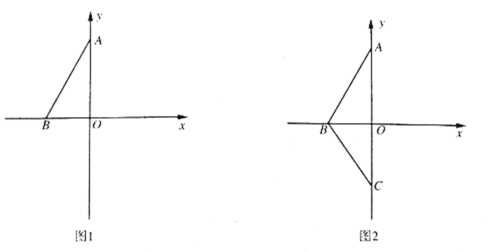
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,并且
,并且![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)把![]() 沿着
沿着![]() 轴折叠得到
轴折叠得到![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位的速度运动.设点
个单位的速度运动.设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含有
,请用含有![]() 的式子表示
的式子表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
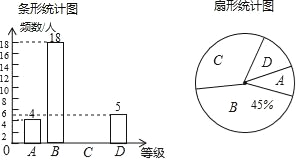
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,有如下探讨:
甲同学:我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学:我知道边数为3时,它是正三角形;我想,边数为5时,它可能也是正五边形…
丙同学:我发现边数为6时,它也不一定是正六边形.如图2,△ABC是正三角形,弧AD、弧BE、弧CF均相等,这样构造的六边形ADBECF不是正六边形.
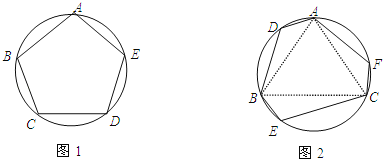
(1)如图1,若圆内接五边形ABCDE的各内角均相等,则∠ABC= °,并简要说明圆内接五边形ABCDE为正五边形的理由;
(2)如图2,请证明丙同学构造的六边形各内角相等;
(3)根据以上探索过程,就问题“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3,n为整数)”的关系,提出你的猜想(不需证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com