
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
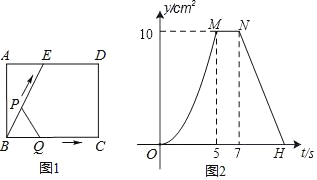
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
【答案】(1)5;(2)![]() ;
;
【解析】
(1)根据图2可得,当点P到达点E时,点Q到达点C,从而可求出BC=BE=5cm;
(2)过点P作PF⊥BC于点F,根据面积不变时△BPQ的面积为10,可得AB=4,利用三角函数求出PF的长,再结合勾股定理求解即可.
解:(1)根据图2可得,当点P到达点E时,点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm.
故答案是:5;
(2)如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=![]() =
=![]() ,
,
∴PF=PBsin∠PBF=2.5×![]() =2,
=2,
∴在直角△PBF中,由勾股定理得到:BF=![]() =
=![]() =1.5,
=1.5,
∴FQ=2.5﹣1.5=1.
∴在直角△PFQ中,由勾股定理得到:PQ=![]() =
=![]() =
=![]() .
.
故答案是:![]() .
.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
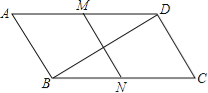
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
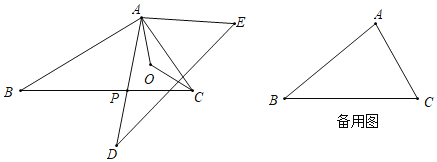
【题目】如图,在△ABC和△ADE中,点P是线段BC上的动点(P不与B、C重合),且AD经过P点;已知∠B=∠D=30°,BC=DE,AB=AD=10,∠PAC的平分线与∠ACB的平分线交于O.
(1)∠BAD与∠CAE相等吗?说明其理由;
(2)若AP长为m,请用含m的代数式表示线段PD的长,并求PD的最大值;
(3)当∠BAC=90°时,α°<∠AOC<β°,那么α= ,β= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D是△ABC中∠BAC的平分线和BC的垂直平分线的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
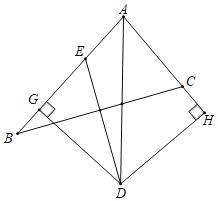
(1)求证:BG=CH;
(2)若AB=12,AC=6,则BG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了![]() ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com