
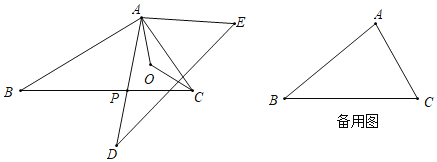
����Ŀ����ͼ���ڡ�ABC�͡�ADE�У���P���߶�BC�ϵĶ��㣨P����B��C�غϣ�����AD����P�㣻��֪��B����D��30�㣬BC��DE��AB��AD��10����PAC��ƽ�������ACB��ƽ���߽���O��
��1����BAD���CAE�����˵�������ɣ�
��2����AP��Ϊm�����ú�m�Ĵ���ʽ��ʾ�߶�PD�ij�������PD�����ֵ��
��3������BAC��90��ʱ�����㣼��AOC�����㣬��ô������ ���������� ����
���𰸡���1����BAD����CAE������������2��PD��10��m��5����3��105,150
��������
��1��������SAS֤����ABC�ա�ADE��Ȼ��ó���BAC����DAE��ͨ�������������ɵó���BAD����CAE��
��2��PD��AD��AP��10��m���ɵ�P���߶�BC���Ҳ���B��C�غϣ��ó�AP����Сֵ��AP��BCʱAP�ij��ȣ���ʱPD�ɵ����ֵ��
��3��OΪ��APC��ƽ���ߵĽ��㣬Ӧ�á��������ڽǺ͵���180�㡰����ƽ���߶��弴�ɱ�ʾ����AOC���Ӷ��õ���������ֵ��
�⣺��1����BAD����CAE���������£�
��ͼ��ʾ��
�ڡ�ABC�͡�ADE�У�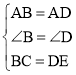 ��
��
���ABC�ա�ADE��SAS��
���BAC����DAE
����BAD+��DAC����DAC+��CAE
���BAD����CAE��
��2����AD��10��AP��m��
��PD��10��m
��AD��BCʱ��AP��С����PD���
![]()
��AP��![]() AB��5��
AB��5��
��PD��10��5��5
��PD�����ֵΪ5��
��3����ͼ2�����BAP��![]() �����APC��
�����APC��![]() ��
��
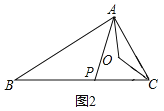
��AB��AC��![]() ��
��
���BAC��90�㣬��PCA��60�㣬��PAC��![]() ��
��
�ߡ�PAC��ƽ�������ACB��ƽ���߽���O��
���OAC��![]() ��PAC����OCA��
��PAC����OCA��![]() ��PCA
��PCA
��![]()
![]()
![]()
![]()
![]()
![]()
��![]()
������105������150��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AD�ǡ�BAC�Ľ�ƽ���ߡ�
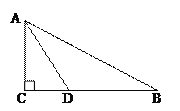
(1)��AB��һ��OΪԲ�ģ�ADΪ������O;
(2)��֤��BCΪ��O�����ߣ�
(3)���AC=3,tanB=![]() ,���O�İ뾶��
,���O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
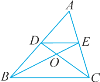
����Ŀ����ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬����BE,CD�ཻ�ڵ�O������DE�����н��ۣ���![]() =
=![]() ;��
;��![]() =
=![]() ;��
;��![]() =
=![]() ;��
;��![]() =
=![]() ��������ȷ�ĸ����У� ��
��������ȷ�ĸ����У� ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
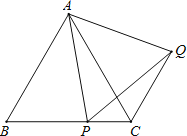
��1����֤��![]() ��
��
��2��![]() ��
��![]() �ܷ��ഹֱ�����ܻ��ഹֱ��ָ����
�ܷ��ഹֱ�����ܻ��ഹֱ��ָ����![]() ��
��![]() �ϵ�λ�ã�������֤������
�ϵ�λ�ã�������֤������![]() ��
��![]() ���ܴ�ֱ����˵�����ɣ�
���ܴ�ֱ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
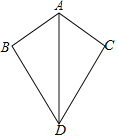
����Ŀ����ͼ�����������������ϵ
��AB��AC����BD��CD���ۡ�BAD����CAD���ܡ�B����C��90�㣻�ݡ�BDA����CDA��
��������������Ϊ�������������е�һ��Ϊ���ۣ�д��һ����ȷ���⣨ֻ��д��һ���������������֤����
�⣺��ѡ��Ϊ����ĵ�����ϵ�ǣ��� ������ ����
��Ϊ��ȷ���۵ĵ�����ϵ���� ����
֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1,��ABC�͡�DEF���������ȫ�غϵ����ǰ�,![]() ,
,![]() .����ͼ1��ʾ��״̬��,��DEF�̶�����,����ABC��ֱ��a����ƽ��.
.����ͼ1��ʾ��״̬��,��DEF�̶�����,����ABC��ֱ��a����ƽ��.
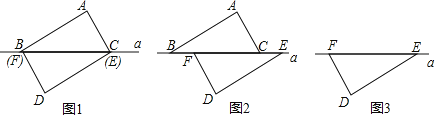
(1)����ABC�Ƶ�ͼ2λ��ʱ,����AF��DC,��֤:AF=DC��
(2)��EF=8,������ƽ�ƹ�����,�Բ����C���E��Զʱ,�߶�AD��ֱ��a��ֱƽ�֡���֤����IJ�������ȷ�ġ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������[a��b��c]Ϊ����y=ax2+bx+c�����������������������Ϊ[m��1��1+m����2m]�ĺ�����һЩ���ۣ��ٵ�m=3ʱ������ͼ��Ķ��������ǣ���1����8�����ڵ�m��1ʱ������ͼ���x�����õ��߶γ��ȴ���3���۵�m��0ʱ��������x��![]() ʱ��y��x���������С���ܲ���mȡ��ֵ������ͼ���������㣮������ȷ�Ľ����У�������
ʱ��y��x���������С���ܲ���mȡ��ֵ������ͼ���������㣮������ȷ�Ľ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ��EΪ����ABCD�ı�AD��һ�㣬����P��Qͬʱ�ӵ�B��������P������BE��ED��DC�˶�����Cʱֹͣ����Q��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/�룬��P��Qͬʱ����t��ʱ����BPQ�����Ϊycm2����֪y��t�ĺ�����ϵͼ����ͼ2��ʾ����ش�
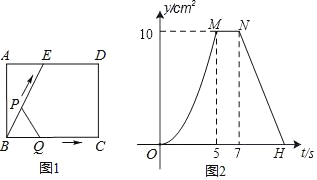
��1���߶�BC�ij�Ϊ �� ��cm��
��2�����˶�ʱ��t=2.5��ʱ��P��Q֮��ľ������� ��cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
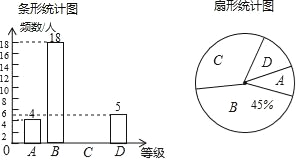
����Ŀ���������������п������ؿ���Ŀ֮һ��������ijѧУΪ�˽������꼶ѧ�������������������������ȡ���־��꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ������²�������ͳ��ͼ����˵����A����8�֩�10�֣�B����7�֩�7.9�֣�C����6�֩�6.9�֣�D����1�֩�5.9�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ�����ε�Բ�Ľ����� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ���������� ���ȼ���
��4����У���꼶��300��ѧ�������������������Գɼ��ﵽA����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com