
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
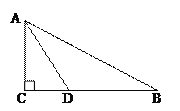
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)由题意可知,作线段AD的垂直平分线与AB相交,交点即为圆心O,然后以O为圆心OA为半径作圆即可;
(2)连接OD,由已知易证∠ODA=∠OAD=∠CAD,从而可得OD∥AC,由此可得∠ODB=∠C=90°,结合OD是⊙O的半径即可得到BC和⊙O相切;
(3)由已知条件易得BC=4和AB=5的长度,设⊙O的半径为r,则OD=OA=r,OB=5-r;由OD∥AC可得△BDO∽△BCA,这样由相似三角形对应边成比例即可列出关于r的方程,解方程即可求得r的值.
试题解析:
(1)如图所示,⊙O为所求圆;
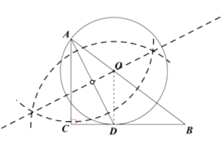
(2)连接OD.
∵AD平分∠CAB
∴∠CAD=∠BAD
又∵OA=OD
∴∠OAD=∠ODA
∴∠CAD=∠ODA
∴OD∥AC
∴∠ODB=∠C=90°
又∵OD为半径
∴BC是⊙O的切线.
(3)∵在△ABC中,AC=3,tanB=![]() ,∠C=90°,
,∠C=90°,
∴BC=4,AB=5,
设⊙O的半径为r,则OA=OD=r,BO=5-r
∵OD∥AC
∴△BOD∽△BAC
∴![]()
即 ![]()
解得, ![]() ,
,
∴⊙O的半径为 ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
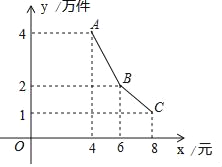
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.
(1)求第一次每个书包的进价是多少元?
(2)若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包按同一标准一次性打折销售,但要求这次的利润不少于480元,问最低可打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第七届世界军人运动会(![]() )于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示:
)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示:
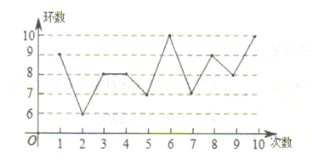
下列结论中不正确的有( )个.①众数是8;②中位数是8;③平均数是8;④方差是1.6.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
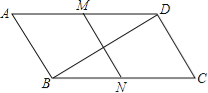
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
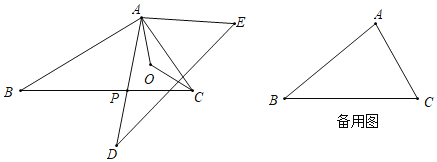
【题目】如图,在△ABC和△ADE中,点P是线段BC上的动点(P不与B、C重合),且AD经过P点;已知∠B=∠D=30°,BC=DE,AB=AD=10,∠PAC的平分线与∠ACB的平分线交于O.
(1)∠BAD与∠CAE相等吗?说明其理由;
(2)若AP长为m,请用含m的代数式表示线段PD的长,并求PD的最大值;
(3)当∠BAC=90°时,α°<∠AOC<β°,那么α= ,β= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com