【题目】某商店第一次用3000元购进某款书包，很快卖完，第二次又用2400元购进该款书包，但这次每个书包的进价是第一次进价的1.2倍，数量比第一次少了20个.
（1）求第一次每个书包的进价是多少元?
（2）若第二次进货后按80元/个的价格销售，恰好销售完一半时，根据市场情况，商店决定对剩余的书包按同一标准一次性打折销售，但要求这次的利润不少于480元，问最低可打几折？
科目：初中数学 来源： 题型：
【题目】已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．
（1）操作发现：直线l⊥m，分别交m、n于点A、B，当点B与点D重合时（如图1），连结PA，请直接写出线段PA与PB的数量关系： ．
（2）猜想证明：在图1的情况下，把直线l向右平移到如图2的位置，试问（1）中的PA与PB
的关系式是否仍然成立？若成立，请给予证明；若不成立，请说明理由．
（3）延伸探究：在图2的情况下，把直线l绕点A旋转，使得∠APB=90°（如图3），若两平行线m、n之间的距离为2k，求证：PAPB=kAB．
查看答案和解析>>
科目：初中数学 来源： 题型：
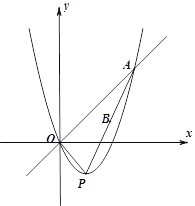
【题目】如图，已知直线
与二次函数
的图像交于点A、O，(O是坐标原点)，点P为二次函数图像的顶点，OA=
，AP的中点为B．
（1）求二次函数的解析式；
（2）求线段OB的长；
（3）若射线OB上存在点Q，使得△AOQ与△AOP相似，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：
亮亮服装店销售一种服装，若按原价销售，则每月销售额为10000元；若按八五折销售，则每月多卖出20件，且月销售额还增加1900元．
（1）求每件服装的原价是多少元？
（2）若这种服装的进价每件150元，求按八五折销售的总利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线。
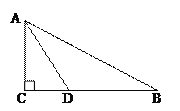
(1)以AB上一点O为圆心，AD为弦作⊙O;
(2)求证：BC为⊙O的切线；
(3)如果AC=3,tanB=
,求⊙O的半径。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（ ）
A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校积极开展“我爱我的祖国”教育知识竞赛，八年级甲、乙两班分别选5名同学参加比赛，其预赛成绩如图所示：
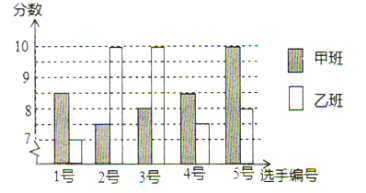
（1）根据上图填写下表：
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
（2）根据上表数据，分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析．
查看答案和解析>>
科目：初中数学 来源： 题型：
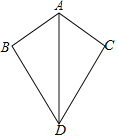
【题目】如图给出下列五个等量关系
①AB＝AC；②BD＝CD；③∠BAD＝∠CAD；④∠B＝∠C＝90°；⑤∠BDA＝∠CDA．
请你以其中两个为条件，另三个中的一个为结论，写出一个正确命题（只需写出一种情况），并加以证明．
解：我选作为题设的等量关系是： 、 ；
作为正确结论的等量关系是 ．
证明：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
