
【题目】 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
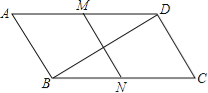
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
【答案】见解析
【解析】
试题(1)根据平行四边形的性质,可得AD与BC的关系,根据MD与NC的关系,可得证明结论;
(2)根据根据等边三角形的判定与性质,可得∠DNC的度数,根据三角形外角的性质,可得∠DBC的度数,根据正切函数,可得答案.
证明:(1)∵ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵M、N分别是AD、BC的中点,
∴MD=NC,MD∥NC,
∴MNCD是平行四边形;
(2)如图:连接ND,
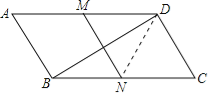
∵MNCD是平行四边形,
∴MN=DC.
∵N是BC的中点,
∴BN=CN,
∵BC=2CD,∠C=60°,
∴△NCD是等边三角形.
∴ND=NC,∠DNC=60°.
∵∠DNC是△BND的外角,
∴∠NBD+∠NDB=∠DNC,
∵DN=NC=NB,
∴∠DBN=∠BDN=![]() ∠DNC=30°,
∠DNC=30°,
∴∠BDC=90°.
∵tan![]() ,
,
∴DB=![]() DC=
DC=![]() MN.
MN.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
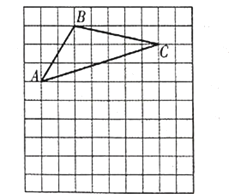
【题目】如图,已知△ABC的其中两个顶点分别为:A(-4,1)、B(-2,4).
(1)请根据题意,在图中建立平面直角坐标系,并写出点C的坐标;
(2)若△ABC每个点的横坐标保持不变,纵坐标分别乘-1,顺次连接这些点,得到△A1B1C1,画出△A1B1C1,判断△A1B1C1与△ABC有怎样的位置关系?并写出点B的对应点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
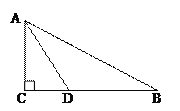
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
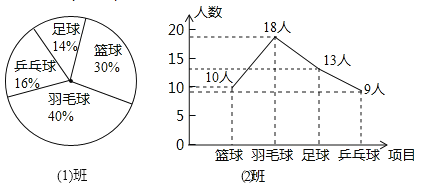
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“我爱我的祖国”教育知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其预赛成绩如图所示:
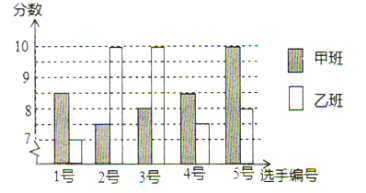
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)5x>4x+8 (2)x+2<-1 (3)-![]() x>-1
x>-1
(4)10-x>0 (5)-![]() x<-2 (6)3x+5<0
x<-2 (6)3x+5<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,连接BE,CD相交于点O,连接DE,下列结论:①![]() =
=![]() ;②
;②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() ,其中正确的个数有( )
,其中正确的个数有( )
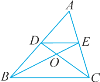
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 上一点,
上一点,![]() 为等边三角形.
为等边三角形.
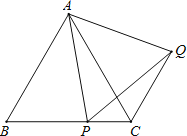
(1)求证:![]() ;
;
(2)![]() 与
与![]() 能否互相垂直?若能互相垂直,指出点
能否互相垂直?若能互相垂直,指出点![]() 在
在![]() 上的位置,并给予证明;若
上的位置,并给予证明;若![]() 与
与![]() 不能垂直,请说明理由.
不能垂直,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
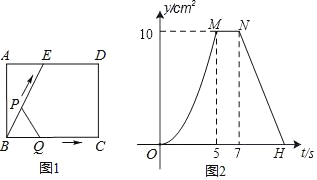
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com