
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 上一点,
上一点,![]() 为等边三角形.
为等边三角形.
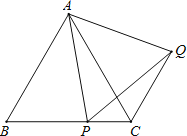
(1)求证:![]() ;
;
(2)![]() 与
与![]() 能否互相垂直?若能互相垂直,指出点
能否互相垂直?若能互相垂直,指出点![]() 在
在![]() 上的位置,并给予证明;若
上的位置,并给予证明;若![]() 与
与![]() 不能垂直,请说明理由.
不能垂直,请说明理由.
【答案】(1)见解析;(2)AQ与CQ能互相垂直,此时点P在BC的中点
【解析】
(1)根据等边三角形性质得出AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,求出∠BAP=∠CAQ,根据SAS证△ABP≌△ACQ,推出∠ACQ=∠B=60°=∠BAC,根据平行线的判定推出即可.
(2)根据等腰三角形性质求出∠BAP=30°,求出∠BAQ=90°,根据平行线性质得出∠AQC=90°,即可得出答案.
(1)证明:∵△ABC和△APQ是等边三角形,
∴AB=AC,AP=AQ,∠BAC=∠B=∠PAQ=60°,
∴∠BAP=∠CAQ=60°-∠PAC,
在△ABP和△ACQ中,
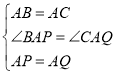 ,
,
∴△ABP≌△ACQ(SAS),
∴∠ACQ=∠B=60°=∠BAC,
∴AB∥CQ;
(2)AQ与CQ能互相垂直,此时点P在BC的中点,
证明:∵当P为BC边中点时,∠BAP=![]() ∠BAC=30°,
∠BAC=30°,
∴∠BAQ=∠BAP+∠PAQ=30°+60°=90°,
又∵AB∥CQ,
∴∠AQC=90°,
即AQ⊥CQ.


科目:初中数学 来源: 题型:
【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
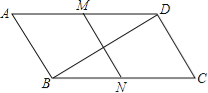
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
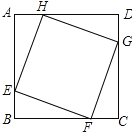
A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
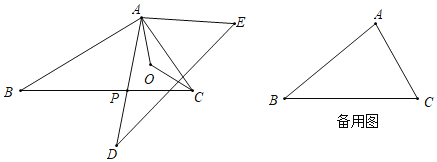
【题目】如图,在△ABC和△ADE中,点P是线段BC上的动点(P不与B、C重合),且AD经过P点;已知∠B=∠D=30°,BC=DE,AB=AD=10,∠PAC的平分线与∠ACB的平分线交于O.
(1)∠BAD与∠CAE相等吗?说明其理由;
(2)若AP长为m,请用含m的代数式表示线段PD的长,并求PD的最大值;
(3)当∠BAC=90°时,α°<∠AOC<β°,那么α= ,β= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com