
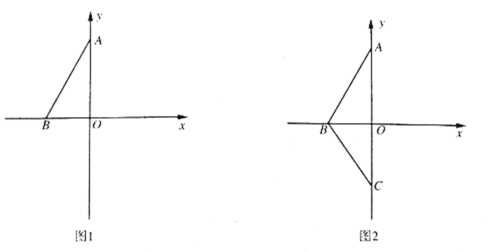
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,并且
,并且![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)把![]() 沿着
沿着![]() 轴折叠得到
轴折叠得到![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位的速度运动.设点
个单位的速度运动.设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含有
,请用含有![]() 的式子表示
的式子表示![]() .
.
【答案】(1)A(0,4),B(-3,0);(2)①当点P在线段BC上时,![]() ;②当点P在线段BC延长线上时,
;②当点P在线段BC延长线上时,![]()
【解析】
(1)将代数式化简,利用非负性质求出a、b的值即可求出A、B的坐标.
(2)先求出C点坐标, 过点P作PM ⊥y轴,用t表示PM的长度,分别讨论P在BC上和P在BC延长线上的情况.
解:(1)∵a-4|+b2+6b+9=0,
∴ a-4=0,b2+6b+9=(b+3)2=0,
∴ a=4, b=-3,
∴A(0,4),B(-3,0).
(2)由折叠可知C(0,-4),
∠BCO=∠BAO=30°,
∴OB=3,OC=4,
过点P作PM ⊥y轴,垂足为M,
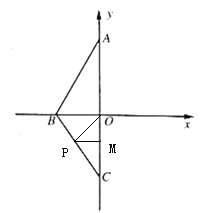
∴![]() .
.
①当点P在线段BC上时:
![]() .
.
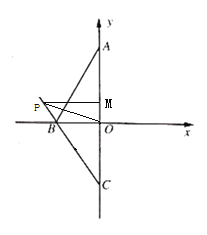
②当点P在线段BC延长线上时:
![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D是△ABC中∠BAC的平分线和BC的垂直平分线的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
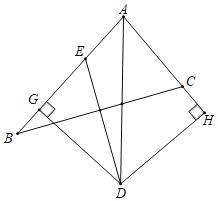
(1)求证:BG=CH;
(2)若AB=12,AC=6,则BG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OA1B1绕点O逆时针旋转90°,得△OA2B2;△OA2B2绕点O逆时针旋转90°,得△OA3B3;△OA3B3绕点O逆时针旋转90°,得△OA4B4;…;若点A1(1,0),B1(1,1),则点B4的坐标是________,点B 2018的坐标是________.
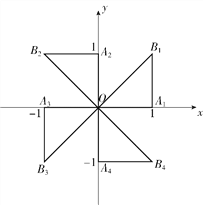
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东海县是“世界水晶之都”,某水晶产业大户经销一种水晶新产品,现准备从国内和国外两种销售方案中选择一种进行销售,若只在国内销售,销售价格y(元/件)与月销售x(件)的函数关系式为y=﹣![]() x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳
x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w2(元).
x2元的附加费,设月利润为w2(元).
(1)当x=1000时,y= 元/件,w1= 元.
(2)分别求出w1,w2与x间的函数关系式(不必写x的取值范围).
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与国内销售月利润最大值相同,求a的值.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨(x>14),应交水费为y元,请写出y与x之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
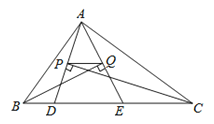
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com