
【题目】如图,在平面直角坐标系xOy中,△OA1B1绕点O逆时针旋转90°,得△OA2B2;△OA2B2绕点O逆时针旋转90°,得△OA3B3;△OA3B3绕点O逆时针旋转90°,得△OA4B4;…;若点A1(1,0),B1(1,1),则点B4的坐标是________,点B 2018的坐标是________.
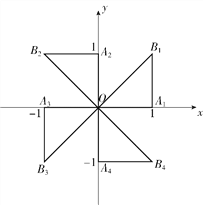
【答案】 点B4的坐标是(1,﹣1), 点B2018的坐标是(﹣1,1).
【解析】
根据旋转的性质结合题目中的已知条件进行分析计算得到点B2、B3、B4的坐标,并由此找到点Bn的坐标在旋转过程中的变化规律即可.
∵点A1、B1的坐标分别为(1,0)、(1,1),
∴OA1=1,A1B1=1,
由旋转的性质可得:OA4=OA3=OA2=OA1=1,A4B4=A3B3=A2B2=A1B1=1,
∴B2的坐标为(-1,1)、B3的坐标为(-1,-1)、B4的坐标为(1,-1),
∵![]() ,
,
∴点B2018与点B2重合,
∴点B2018的坐标为(-1,1).
故答案为:(1)(1,-1);(2)(-1,1).


科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.

(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
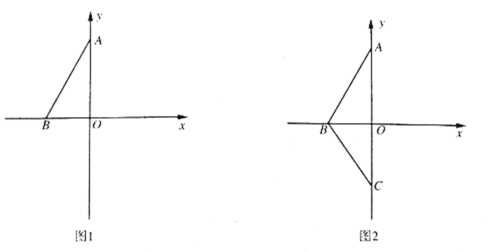
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,并且
,并且![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)把![]() 沿着
沿着![]() 轴折叠得到
轴折叠得到![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位的速度运动.设点
个单位的速度运动.设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含有
,请用含有![]() 的式子表示
的式子表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
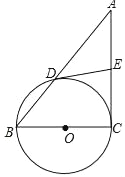
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AB=25,DE=10,弧DC的长为a,求DE、EC和弧DC围成的部分的面积S.(用含字母a的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com