
【题目】东海县是“世界水晶之都”,某水晶产业大户经销一种水晶新产品,现准备从国内和国外两种销售方案中选择一种进行销售,若只在国内销售,销售价格y(元/件)与月销售x(件)的函数关系式为y=﹣![]() x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳
x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w2(元).
x2元的附加费,设月利润为w2(元).
(1)当x=1000时,y= 元/件,w1= 元.
(2)分别求出w1,w2与x间的函数关系式(不必写x的取值范围).
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与国内销售月利润最大值相同,求a的值.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
【答案】(1)80,43750;(2)w1=﹣![]() x2+150x﹣6250,w2=(180﹣a)x﹣
x2+150x﹣6250,w2=(180﹣a)x﹣![]() x2;(3)当x为750时,在国内销售的利润最大,若在国外销售月利润的最大值与国内销售月利润最大值相同,a的值为40.
x2;(3)当x为750时,在国内销售的利润最大,若在国外销售月利润的最大值与国内销售月利润最大值相同,a的值为40.
【解析】
(1)将x=1000代入函数关系式求得y,并根据等量关系“利润=销售额-成本-广告费” 求得![]() ;
;
(2)根据等量关系 “利润=销售额-成本-广告费” “利润=销售额-成本-附加费”列出两个函数关系式;
(3)对![]() 函数的函数关系式求得最大值,再求出
函数的函数关系式求得最大值,再求出![]() 的最大值并令二者相等求得a值.
的最大值并令二者相等求得a值.
解:(1)根据题意得:w1=(y﹣30)x﹣6250=﹣![]() x2+150x﹣6250,
x2+150x﹣6250,
把x=1000代入y=﹣![]() x+180得:y=﹣
x+180得:y=﹣![]() ×1000+180=80,
×1000+180=80,
把x=1000代入w1=﹣![]() x2+150x﹣6250得:w1=﹣
x2+150x﹣6250得:w1=﹣![]() ×10002+150×1000﹣6250=43750
×10002+150×1000﹣6250=43750
故答案为:80,43750,
(2)由(1)可知:w1=﹣![]() x2+150x﹣6250,
x2+150x﹣6250,
由题意得:w2=(180﹣a)x﹣![]() x2,
x2,
(3)w1=﹣![]() x2+150x﹣6250=﹣
x2+150x﹣6250=﹣![]() (x﹣750)2+50000,
(x﹣750)2+50000,
当x=750时,w1取到最大值50000,
根据题意得:w2(最大)=![]() =50000,
=50000,
解得:a1=320(舍去),a2=40,
故当x为750时,在国内销售的利润最大,若在国外销售月利润的最大值与国内销售月利润最大值相同,a的值为40.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
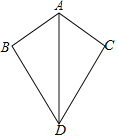
【题目】如图给出下列五个等量关系
①AB=AC;②BD=CD;③∠BAD=∠CAD;④∠B=∠C=90°;⑤∠BDA=∠CDA.
请你以其中两个为条件,另三个中的一个为结论,写出一个正确命题(只需写出一种情况),并加以证明.
解:我选作为题设的等量关系是: 、 ;
作为正确结论的等量关系是 .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
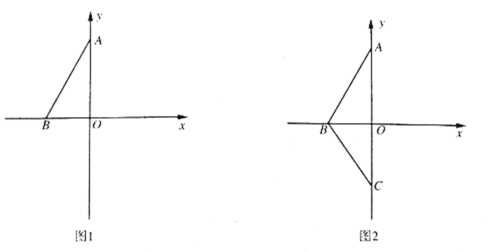
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,并且
,并且![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)把![]() 沿着
沿着![]() 轴折叠得到
轴折叠得到![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位的速度运动.设点
个单位的速度运动.设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含有
,请用含有![]() 的式子表示
的式子表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
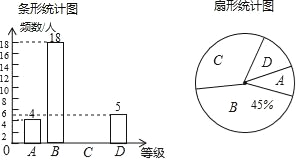
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
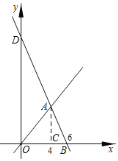
【题目】如图,一次函数的图象交x轴于点B (6,0),交正比例函数的图象于点A,且点A的横坐标为4,S△ABO=12.求一次函数和正比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
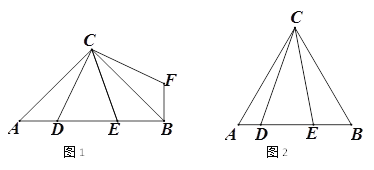
【题目】如图,△ABC中AC=BC,点D,E在AB边上,连接CD,CE.
(1)如图1,如果∠ACB=90°,把线段CD逆时针旋转90°,得到线段CF,连接BF,
①求证:△ACD≌△BCF;
②若∠DCE=45°, 求证:DE2=AD2+BE2;
(2)如图2,如果∠ACB=60°,∠DCE=30°,用等式表示AD,DE,BE三条线段的数量关系,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com