
【题目】如图,△ABC中AC=BC,点D,E在AB边上,连接CD,CE.
(1)如图1,如果∠ACB=90°,把线段CD逆时针旋转90°,得到线段CF,连接BF,
①求证:△ACD≌△BCF;
②若∠DCE=45°, 求证:DE2=AD2+BE2;
(2)如图2,如果∠ACB=60°,∠DCE=30°,用等式表示AD,DE,BE三条线段的数量关系,说明理由.
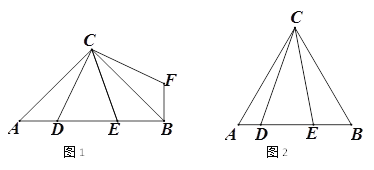
【答案】(1)①详见解析;②详见解析;(2)DE2= EB2+AD2+EB·AD,证明详见解析
【解析】
(1)①根据旋转的性质可得CF=CD,∠DCF=90°,再根据已知条件即可证明△ACD≌△BCF;
②连接EF,根据①中全等三角形的性质可得∠EBF=90°,再证明△DCE≌△FCE得到EF=DE即可证明;
(2)根据(1)中的思路作出辅助线,通过全等三角形的判定及性质得出相等的边,再由勾股定理得出AD,DE,BE之间的关系.
解:(1)①证明:由旋转可得CF=CD,∠DCF=90°
∵∠ACD=90°
∴∠ACD=∠BCF
又∵AC=BC
∴△ACD≌△BCF
②证明:连接EF,
由①知△ACD≌△BCF
∴∠CBF=∠CAD=∠CBA=45°,∠BCF=∠ACD,BF=AD
∴∠EBF=90°
∴EF2=BE2+BF2,
∴EF2=BE2+AD2
又∵∠ACB=∠DCF=90°,∠CDE=45°
∴∠FCE=∠DCE=45°
又∵CD=CF,CE=CE
∴△DCE≌△FCE
∴EF=DE
∴DE2= AD2+BE2
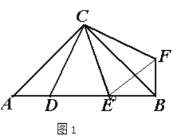
⑵DE2= EB2+AD2+EB·AD
理由:如图2,将△ADC绕点C逆时针旋转60°,得到△CBF,过点F作FG⊥AB,交AB的延长线于点G,连接EF,
∴∠CBE=∠CAD,∠BCF=∠ACD, BF=AD
∵AC=BC,∠ACB=60°
∴∠CAB=∠CBA =60°
∴∠ABE=120°,∠EBF=60°,∠BFG=30°
∴BG=![]() BF,FG=
BF,FG=![]() BF
BF
∵∠ACB=60°,∠DCE=30°,
∴∠ACD+∠BCE=30°,
∴∠ECF=∠FCB+∠BCE=30°
∵CD=CF,CE=CE
∴△ECF≌△ECD
∴EF=ED
在Rt△EFG中,EF2=FG2+EG2
又∵EG=EB+BG
∴EG=EB+![]() BF,
BF,
∴EF2=(EB+![]() BF)2+(
BF)2+(![]() BF)2
BF)2
∴DE2= (EB+![]() AD)2+(
AD)2+(![]() AD)2
AD)2
∴DE2= EB2+AD2+EB·AD


科目:初中数学 来源: 题型:
【题目】东海县是“世界水晶之都”,某水晶产业大户经销一种水晶新产品,现准备从国内和国外两种销售方案中选择一种进行销售,若只在国内销售,销售价格y(元/件)与月销售x(件)的函数关系式为y=﹣![]() x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳
x+180,成本为30元/件,无论销售多少,每月还需支出广告费6250元,设月利润为w1(元),若只在国外销售,销售价格为180元/件,受各种不确定因素影响,成本为a元/件(a为常数,20≤a≤60),当月销售量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w2(元).
x2元的附加费,设月利润为w2(元).
(1)当x=1000时,y= 元/件,w1= 元.
(2)分别求出w1,w2与x间的函数关系式(不必写x的取值范围).
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与国内销售月利润最大值相同,求a的值.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2).
≈2.2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),
D(-2,-2),E(0,-3)。

(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(-2,-2),E(0,-3),判断直线l与⊙P的位置关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
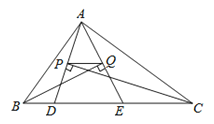
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解答题:
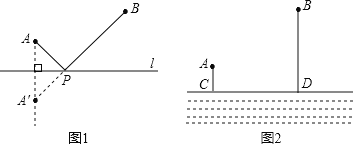
(几何概型)
条件:如图1:![]() 是直线
是直线![]() 同旁的两个定点.
同旁的两个定点.
问题:在直线![]() 上确定一点
上确定一点![]() ,使
,使![]() 的值最小;
的值最小;
方法:作点![]() 关于直线
关于直线![]() 对称点
对称点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
由“两点之间,线段最短”可知,点![]() 即为所求的点.
即为所求的点.
(模型应用)
如图2所示:两村![]() 在一条河
在一条河![]() 的同侧,
的同侧,![]() 两村到河边
两村到河边![]() 的距离分别是
的距离分别是![]() 千米,
千米,![]() 千米,
千米, ![]() 千米,现要在河边
千米,现要在河边![]() 上建造一水厂,向
上建造一水厂,向![]() 两村送水,铺设水管的工程费用为每千米20000元,请你在
两村送水,铺设水管的工程费用为每千米20000元,请你在![]() 上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用
上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用![]() .
.
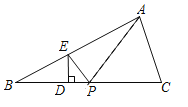
(拓展延伸)
如图,![]() 中,点
中,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一个动点,连接
上一个动点,连接![]() ,若
,若![]() 最小,则点
最小,则点![]() 应该满足( )(唯一选项正确)
应该满足( )(唯一选项正确)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区![]() . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形![]() 的边
的边![]() 米,面积为
米,面积为![]() 平方米.
平方米.
(1)请写出活动区面积![]() 与
与![]() 之间的关系式,并指出
之间的关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com