
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

【答案】(1)![]() ;(2)①
;(2)①![]() ,②6.
,②6.
【解析】
试题分析:(1)根据辅助线的作法可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得![]() =
=![]() ;(2)①过点A作AF∥DB,交BE的延长线于点F,可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得
;(2)①过点A作AF∥DB,交BE的延长线于点F,可得△AEF≌△CEB,△AFP∽△DBP,然后利用它们的性质可得![]() =
=![]() ;②根据条件DC:BC:AC=1:2:3 ,CD=2,得出BC, AC,CE,AE的长,由勾股定理可得 EF的长,再利用△AFP∽△DBP的性质可求出BP的长.
;②根据条件DC:BC:AC=1:2:3 ,CD=2,得出BC, AC,CE,AE的长,由勾股定理可得 EF的长,再利用△AFP∽△DBP的性质可求出BP的长.
试题解析:(1)![]() 的值为
的值为![]() .
.
(2)①过点A作AF∥DB,交BE的延长线于点F,
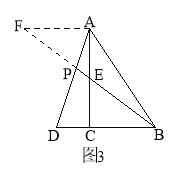
∵DC︰BC=1︰2,
∴BC=2k.
∴DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
又∵∠2=∠3,
∴△AEF≌△CEB.
∴AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP.
∴![]() .
.
∴![]() =
=![]() .
.
②∵DC:BC:AC=1:2:3 ,CD=2,∴BC=4 AC=6
∴ CE=AE=![]() AC =3
AC =3
∴ 由勾股定理可得: EF=5,∴BF=10
∵ ![]() =
=![]() ,△AFP∽△DBP,
,△AFP∽△DBP,
∴![]()
∴BP=6


科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处.
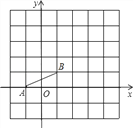
(1)写出点C的坐标__________;
(2)求经过C、D的直线与y轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔出一名参加射击比赛,现对他们的射击水平进行一次测验,两个人在相同条件下各射靶10次,为了比较两个人的成绩,制作了如下统计图表:
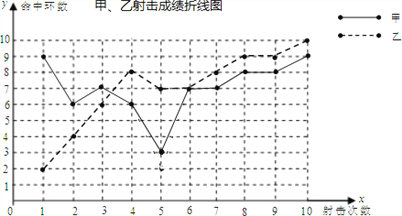
甲、乙射击成绩统计表

(1)请补全上述统计表.
(2)如果规定成绩较稳定者胜出,你认为谁胜出?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
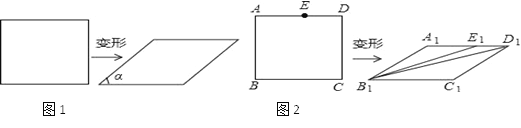
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2﹣y2=(x﹣y)2 B. xy﹣x=x(y﹣1)
C. a2+a+1=(a+1)2 D. 2x+y=2(x+y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com