
【题目】阅读理解:
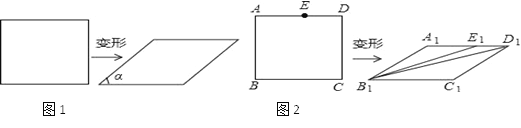
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)∠A1E1B1+∠A1D1B1=30°.
,理由见解析;(3)∠A1E1B1+∠A1D1B1=30°.
【解析】解:(1)![]() ;
;
(2)![]() =
=![]() ,
,
理由:如图1,
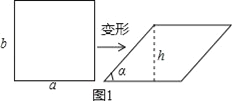
设矩形的长和宽分别为a,b,变形后的平行四边形的高为h,
∴S1=ab,S2=ah,∴![]() =
=![]() =
=![]() ,
,
∵sinα=![]() ∴
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ;
;
(3)∵AB2=AEAD,
∴A1B12=A1E1A1D1,即![]() =
=![]() ,
,
∵∠B1A1E1=∠D1A1B1,∴△B1A1E1∽△D1A1B1,
∴∠A1B1E1=∠A1D1B1,
∵A1D1∥B1C1,
∴∠A1E1B1=∠C1B1E1,
∴∠A1E1B1+∠A1D1B1=∠C1E1B1+∠A1B1E1=∠A1B1C1,
由(2)知![]() =
=![]() 可知
可知![]() =
=![]() =2,
=2,
∴sin∠A1B1C1=![]() ,
,
∴∠A1B1C1=30°,
∴∠A1E1B1+∠A1D1B1=30°.


科目:初中数学 来源: 题型:
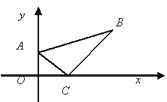
【题目】如图,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系内有一动点P(不与A重合),以P、B、C为顶点的三角形和△ABC全等,则P点坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高台县为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;巷道镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=-1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是-1≤x<3 ;
⑤当x<0时,y随x增大而增大;
其中正确的个数是 ( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组数据为边长,可以构成等腰三角形的是( )
A.1cm、2cm、3cmB.3cm、 3cm、 4cm
C.1cm、3cm、1cmD.2cm、 2cm、 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
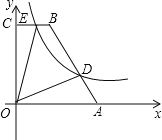
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com